Задумывались ли вы когда-нибудь о том, сколько парадоксов вокруг нас? Сначала нас ставят в тупик требования родителей: «Закрой рот и ешь». Потом вызывают недоумение требования учителей, которые хотят, чтобы мы хорошо знали все школьные предметы, а сами знают только один: тот, который преподают сами.
Во взрослой жизни нас и вовсе ждет разрыв шаблона: рождаемость падает, смертность растет, а жилье с каждым годом дороже и дороже. Но если данный парадокс еще можно как-то объяснить инфляцией и жадностью застройщиков, так называемые логические парадоксы не так-то просто одолеть.
Вам будет проще со всем этим справиться, если вы пройдете нашу программу «Когнитивистика». А сегодня мы пополним копилку ваших «парадоксальных» знаний и поговорим про парадокс двух конвертов.
Парадокс двух конвертов: что это такое?
Парадокс двух конвертов – это логическая задачка, сбившая с толку немало математиков со стажем и обычных людей. Кратко суть парадокса двух конвертов в следующем:
- Есть два одинаковых на вид конверта с деньгами, в одном из которых сумма в два раза больше, чем во втором.
- Приглашаются двое испытуемых, каждый из которых может вскрыть один конверт и увидеть, сколько там денег.
- Каждый из испытуемых знает, что во втором конверте денег в два раза больше либо в два раза меньше, но не знает, достался ему «больший» конверт или «меньший».
- Точно так же второй участник испытания не знает, сколько денег в первом конверте.
- Участники эксперимента могут оставить конверт с деньгами себе или по взаимному согласию поменяться конвертами, и тогда у них на руках окажется сумма в два раза больше или в два раза меньше первоначальной.
Гипотетически шансы выиграть или проиграть равны. В чем тогда парадокс? Чисто математически, парадокс в том, что каждый из участников считает, что обмен ему… выгоден! Как такое может быть, если теория вероятностей прямо указывает на то, что в ситуации с двумя конвертами шансы выиграть составляют 50 на 50?
Если денежную сумму в «своем» конверте условно принять за «х» (икс), тогда во втором конверте будет 0,5х либо 2х. Вероятность выиграть или проиграть равновелика, поэтому на свет рождается следующая формула:
(2х + 0.5х) / 2 = 1.25х
Чтобы было понятно, как это раскрывает суть парадокса двух конвертов, поясним, что каждый из участников потенциально выигрывает на 25% больше, чем проигрывает. Условно говоря, если у вас в руках 100 рублей, в случае проигрыша вы потеряете 50 рублей, а в случае выигрыша получите еще 100 рублей, итого 200 рублей.
Точно ли из этого следует, что меняться в подобной ситуации однозначно выгодно? Здравый смысл подсказывает, что тут речь не о какой-то однозначной выгоде, а скорее о везении или невезении. Но прежде, чем мы перейдем к попыткам решить этот парадокс, сделаем небольшой исторический экскурс.
Парадокс двух конвертов: немного истории
Парадокс двух конвертов в сформулированном выше виде появился не сразу. Впервые он был представлен в 1953 году бельгийским математиком российского происхождения Морисом Крайчиком (1882-1957) в несколько ином варианте и назывался «Парадокс обмена» [M. Kraïtchik, 1953].
Согласно первоначальному условию задачи, двум респектабельным джентльменам предлагалось поменяться кошельками вслепую, не имея понятия, будет в чужом кошельке больше денег или меньше. Не будем снова углубляться в расчеты, потому что суть прежняя: оба джентльмена полагают обмен выгодным.
Данный парадокс достаточно долго кочевал из сборника в сборник в первоначальном варианте с кошельками. Так, эту задачку можно найти в книге Aha! Gotcha: paradoxes to puzzle and delight («Ага! Попался: парадоксы, которые озадачивают и восхищают») [M. Gardner, 1982].
В современном модифицированном виде парадокс был сформулирован уже в конце 80-х годов 20 века профессором Йельской школы менеджмента Барри Нейлбаффом в его работе Puzzles: Cider in Your Ear, Continuing Dilemma, The Last Shall Be First, and More («Головоломки: сидр в ухе, продолжающаяся дилемма, последние должны быть первыми и многое другое») [B. Nalebuff, 1988].
Так чего же здесь больше: расчетов или эмоций? Что нужно изучать, чтобы понять парадокс двух конвертов: теорию вероятностей или восприятие человека и особенности его психики? Давайте попробуем начать с точных наук.
Математическое решение парадокса двух конвертов
Коль скоро мы изначально занялись расчетами, видится логичным продолжить в том же духе и разобраться с математической составляющей парадокса. Полученное нами в результате первоначальных расчетов значение 1.25х – это не просто соотношение возможного выигрыша к возможному проигрышу.
При бесконечно большом количестве раундов игры, если всегда обменивать конверт, это и есть сумма вашего выигрыша в соответствии с канонами теории вероятностей. Другими словами, вы преумножите первоначально увиденную сумму на четверть.
На самом деле, парадокс двух конвертов – это задачка из теории принятия решений, которая является предметом давних споров. Это контринтуитивная проблема разрешимости между двумя разными состояниями в присутствии неопределенности, когда выигрыш игрока должен быть каким-то образом максимизирован [M. McDonnell, D. Abbott, 2009].
Поиск решения является важным, потому что влияет на наше понимание теории вероятностей, теории принятия решений и оптимизации. И в этом нам может помочь так называемая «стратегия переключения Ковера», когда мы переключаем состояния с вероятностью, что является плавно убывающей функцией наблюдаемого значения одного состояния.
Всем, кому интересно лично вникнуть в нюансы расчетной части, можем рекомендовать статью-первоисточник Randomized switching in the two-envelope problem («Случайное переключение в задаче о двух конвертах») [M. McDonnell, D. Abbott, 2009]. Остальным, кому более интересна практическая составляющая проблематики принятия решений, попытаемся объяснить суть простыми словами.
Итак, попав в ситуацию выбора между двумя конвертами на вышеописанных условиях, следует субъективно оценить полученную сумму, и уже исходя из этой оценки вычислить вероятность выигрыша. Если совсем кратко, то чем больше денег в вашем конверте, тем ниже шансы, что во втором конверте денег в 2 раза больше.
Для проверки своего предположения ученые с помощью цифровых технологий сгенерировали порядка 20 тысяч ситуаций, которые позволили выяснить, что применение стратегии переключения Ковера в среднем позволяет выигрывать больше, чем принимаемое случайным образом решение об обмене.
Более того, ученые утверждают, что им удалось создать простой детерминистский (не вероятностный!) алгоритм принятия решений. Если сумма в конверте меньше некоего условного значения, нужно менять конверты, если больше, обмен производить не нужно. Стратегия переключения, основанная на «пороговом решении» после наблюдения суммы в конверте, весьма работоспособна.
Какое решение должно быть «пороговым»? Как определить это «некое условное значение», после которого нужно оставлять конверт себе и ни в коем случае не менять? Пытливый ум российского человека попытался перевести в конкретные цифры «Парадокс двух конвертов и способ увеличения вероятности выбрать правильный конверт» [Habr, 2013].
Для этого был написан скрипт, способный быстро разыграть бесконечное множество сценариев с конвертами. Автор статьи разыграл миллион комбинаций как для ситуации рандомного выбора менять или не менять конверт, так и для сценария с заданными условиями.
Под заданными условиями предполагался конверт с меньшей суммой в диапазоне от 1 доллара до 1 миллиона долларов и, соответственно, конверт с в два раза большей суммой от 2 долларов до 2 миллионов долларов. Решение об обмене принималось на основании следующих правил:
- Если с первой попытки попадалась большая сумма, конверт не меняли.
- Если среднее арифметическое ранее полученных денег было меньше суммы в конверте, конверт тоже оставляли без дальнейшего обмена.
Во всех остальных случаях конверт обменивали. Миллион различных комбинаций, разыгранных с применением данных правил, привел к следующему результату: 76% выигрышей и 24% проигрышей [Habr, 2013]. Так что накопить больше денег относительно первоначальной суммы вполне реально.
Автор скрипта считает, что данная методика применима ко всем случаям, в том числе к исходному условию парадокса двух конвертов, когда ничего не известно о том, в каком диапазоне будут предложены суммы для многораундового розыгрыша. Для интересующихся уточняется, что скрипт написан на php (версия 5.5.3 stable), а в качестве «железа» был задействован обычный 4-ядерный компьютер.
Однако не все готовы замахнуться на миллион. Можно найти и более скромные варианты вычислений. Так, задав несколько исходных условий, автор пришел к выводу, что меняться можно только до суммы в 26 рублей, а начиная с 27 рублей конверт нужно оставлять себе [А. Мичурин, 2016]. Те, кто знаком с языком программирования Python, могут ознакомиться с полученными вычислениями:
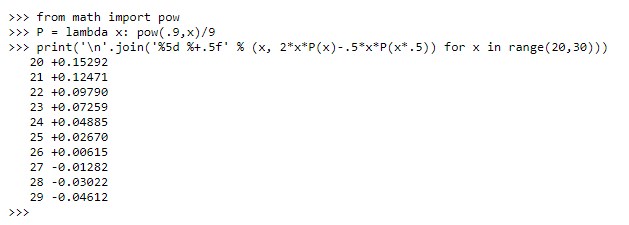
При этом автор скрипта утверждает, что конкретные суммы – это условность, а суть будет одинакова при любых расчетах: обмен выгоден только одной стороне и только до определенной суммы. Второй стороне обмен не выгоден, так что с этой точки зрения никакого парадокса двух конвертов в принципе не существует. А что же тогда существует и заставляет мыслить уже которое поколение аналитиков? Вот это уже вопрос философский!
Философия «Парадокса двух конвертов»
Каждый из нас выбирает каждый день и всю жизнь: что надеть и что съесть, куда пойти учиться и на ком жениться, в какой детский садик отдать ребенка и где ему подобрать подходящую невесту. Иногда мы пытаемся выбирать за других и там, где этого делать не нужно. Например, профессию или вторую половину за своих детей. Но гиперопека – это отдельная тема. А сегодня попытаемся разобраться с темой своего выбора, и не только из двух конвертов.
Автор теории относительности великий ученый Альберт Эйнштейн говорил, что никакую проблему невозможно решить на том уровне, на котором она возникла. Для поиска успешного решения следует подняться на уровень выше. «Пирамида Дилтса» и ее шесть уровней – это как раз о том, как искать решение, поднимаясь как бы «над» проблемой. Поможет ли такой подход применительно к проблеме выбора конвертов? А давайте посмотрим!
Для начала разберемся, на каком уровне возникает эта проблема принятия решения. Первый уровень, согласно Дилтсу, – это базовый уровень и то, что окружает каждого из нас в повседневной жизни. Ключевой вопрос «Что я имею?» Второй уровень отображает наше поведение и отвечает на вопрос «Что я делаю?» Третий уровень объединяет все наши знания, способности и возможности, и ключевой вопрос тут «Как я выбираю?»
Где именно возникает проблема выбора? Может, на первом уровне, когда мы оцениваем, что мы имеем? Ведь каждому хочется иметь больше, не так ли? А если есть легальный способ преумножить доход, не сильно напрягаясь, так почему бы этим не воспользоваться?! Только вот шансов преумножить 50 на 50, и что теперь делать? А сделать нужно выбор, причем мы сейчас не про конверты. Для начала, когда вам предлагают выбор, вам нужно выбрать, принять это предложение или отказаться от него. А уже потом выбирать из двух конвертов.
Как выбирать? Это, как мы помним, вопрос третьего уровня «пирамиды Дилтса». Тогда что там на четвертом? А четвертый уровень – это ценности и убеждения, ключевой вопрос для которого «Во что я верю?» Вы правда верите, что кто-то посторонний собрался вас осчастливить и дать заработать с нулевыми усилиями кругленькую сумму? Вы верите, что сумма в два раза большая, чем та, что у вас в руках, решит все ваши проблемы? Или вы верите в свою удачу и то, что у вас «легкая рука»?
Можно попытаться честно ответить себе на эти вопросы, и тогда многое встанет на свои места. Вам для самого себя станет понятно, как именно делать выбор. Что тогда может вас сдерживать? Например, синдром упущенной выгоды. Ведь речь идет о ситуации выбора, когда равновероятно и получить в два раза больше, и упустить то, что есть, получив в два раза меньше. Вы, разумеется, вряд ли обеднеете, если получите вдвое меньше, чем было у вас в руках изначально.
Однако FOMO (аббревиатура от fear of missing out – страх упустить) штука коварная, и настигает нас даже тогда, когда речь идет не о материальной выгоде, а о веселых посиделках, которые тоже жаль упустить, если быть «не на связи» и вас не успеют позвать. В целом, это тема множества специальных исследований. Итоги одного из таких исследований обобщены в материале Fear of missing out: prevalence, dynamics, and consequences of experiencing FOMO («Страх упустить: распространенность, динамика и последствия FOMO») [Milyavskaya et al, 2018]. Так что если не всегда удается «запастись бесстрашием», не расстраивайтесь, вы не одиноки.
Кстати, тема самоидентификации – это уже пятый уровень «пирамиды Дилтса». Ключевой вопрос «Кто я?» Поможет ли ответ на него быстрее определиться с конвертами? Думается, что да, ведь никто не запрещает искать решение проблемы не только на уровень, но и на два уровня выше, чем тот, на котором она «нарисовалась». Вот, действительно, кто вы? Если вы «халявщик», привыкший все получать «просто так», тогда нервничать в ситуациях такого вот выбора – это ваша судьба. Если вы «пофигист», тогда выбирайте, как угодно, все равно любой исход вы воспримете спокойно. Если вы «везунчик», вам стоит попробовать рискнуть: вдруг повезет и сейчас, раз уж везет постоянно?
А быть может, вы по жизни максималист, для которого «все или ничего» не просто фраза, а стиль жизни? Думается, в этом случае вы не нуждаетесь ни в чьих советах, как вам поступить в ситуации вышеописанного выбора. Как видите разнообразие ответов на такой простой вопрос «Кто я?» уже дает множество ответов, как вам действовать далее.
В принципе, нам остался всего шаг до наивысшего шестого уровня «пирамиды Дилтса», так можем сделать и его. Это высший уровень символизирует миссию человека, его жизненные цели. Ключевой вопрос «Зачем я живу?» Для двух конвертиков звучит несколько пафосно, но суть в другом.
Если каждое свое действие сопоставлять с тем, насколько оно приближает вас к вашим жизненным целям, вы увидите, как много всего не заслуживает не то что ваших переживаний и стрессов, но даже лишних затрат времени и внимания. В этом контексте любая сумма, увиденная вами в конверте, не должна вас стрессировать на предмет шанса увеличить или потерять ее, если она не решает никаких ваших хоть сколько-то существенных задач. А если решает, вот ее и нужно забрать, и нечего претендовать на лишнее.
Даже если вы упустите в какой-то раз возможность заработать, никогда не расстраивайтесь! В этой жизни будет еще очень много возможностей, которые вы тоже упустите. Переживать из-за каждой никаких нервов не хватит, а поскольку все болезни от нервов, нужно всегда помнить, что здоровье важнее.
Кроме того, имеют значения ваши желания, цели и устремления, и вряд ли стоит упускать возможность реализовать их, когда она реально представилась. При таком идейном философском «обрамлении» тема выбора и парадокса двух конвертов видится несколько иначе, и парадокс тут всего один: как много времени мы тратим на размышления о вещах, от которых мало, что зависит?
Быть может, вам поможет книга под неоднозначным названием «Парадокс выбора: почему «больше» значит «меньше» [Б. Шварц, 2005]. В контексте нашей темы интересны буквально несколько мыслей из книги:
- Проблему создает не сам по себе выбор, а многообразие выбора, которое выпадает на нашу долю. Поэтому важно определиться, что действительно имеет большое значение для нас, нашей системы ценностей и наших перспектив, и сосредоточиться исключительно на этом.
- «Ожидаемая реальность» и «вспоминаемая полезность» должны соответствовать друг другу. Проще говоря, не забывайте, что и зачем вы делаете, и не отвлекайтесь на то, что к этому не относится.
В целом, было бы неплохо разобраться и понять, что нам мешает делать выбор [М. Карамазов, 2019]. И тогда мы не запутаемся ни в «Парадоксе двух конвертов», ни в других ситуациях выбора.
Что мешает делать выбор:
- Завышенные ожидания.
- Осведомленность о возможных издержках.
- Неприятие компромиссов.
- Стремление сохранить «статус кво».
- Самобичевание.
- Склонность к сожалениям.
- Сравнение с окружающими.
- Перфекционизм.
На самом деле, перфекционизм и стремление «сделать по максимуму» очень часто мешают двигаться дальше, и не только в деле простого выбора. Казалось бы, чего проще: если сумма в конверте устраивает, так забирайте и будьте довольны! Но нет, все как в ископаемом анекдоте: жили они долго и счастливо, пока не узнали, что многие живут еще дольше и счастливее.
Тема «ловушек восприятия» весьма обширна и требует отдельного рассмотрения, а в рамках нашей статьи выдадим лишь краткие рекомендации психологов, как быть:
- Избавиться от «усталости принятия решений», перестать тратить силы на неважное, уменьшить количество решений, принимаемых постоянно, и помнить лишь о том, что на самом деле важно.
- Создавать «нисходящие контрфактуалы» и вспомнить случаи, когда все закончилось лучше, чем ожидалось. Воспоминаниями о плохом вы себя и так уже достаточно извели.
- Смешать «нисходящие контрфактуалы» и «восходящие контрфактуалы» и не зацикливаться на «могло быть и хуже». А могло и лучше, и для случаев, когда это важно для ваших жизненных целей, это стоит обдумать отдельно.
- Знать и напоминать себе, что вы всегда приспособитесь к новым обстоятельствам, и будете ощущать себя в них комфортно.
- Скорректировать свои ожидания в части того, что каждый ваш выбор не может быть идеальным. Какой-то выбор всегда будет чуть лучше или чуть хуже, иначе относительно какой меры вы уловите момент, когда сделали все безупречно?
- Не перетруждаться там, где ситуация не заслуживает ваших сил и энергии.
- Делать выбор в пределах разумных ограничений.
Последний пункт, пожалуй, стоит пояснить. Не всегда есть возможность получить все и сразу. В контексте нашей темы «Парадокса двух конвертов» не стоит ожидать, что сделанный вами выбор должен решить все ваши материальные проблемы. Поэтому всегда есть смысл остановиться вовремя.
Когда будет это самое вовремя? Мы в самом начале задавались вопросом, что нужно изучать, чтобы понять парадокс двух конвертов: теорию вероятностей или восприятие человека и особенности его психики? И ответим на него так: изучайте нашу программу «Когнитивистика»! Там есть ответы практически на все вопросы, связанные с мышлением.
Как минимум, определите для себя ту сумму, которой вам достаточно, чтобы чувствовать, что вы не зря потратили время на эксперимент с двумя конвертами. И тогда вам не придется тратить нервы.
Мы желаем, чтобы вы обязательно нашли свой баланс сил, времени, энергии и необходимых вам материальных ресурсов. Мы ждем вас на наших курсах и программах, которые в наибольшей степени отвечают вашим чаяниям. И предлагаем ответить на вопрос по теме статьи:
