Вам, конечно же, знакома идея о том, что математика является самой главной из всех наук. Но многие могут с этим не согласиться, т.к. порой кажется, что математика – это лишь задачи, примеры и тому подобная скукотища. Однако математика может запросто показать нам знакомые вещи с совершенно незнакомой стороны. Мало того – она даже может раскрыть тайны мироздания. Как? Давайте обратимся к числам Фибоначчи.
Что такое числа Фибоначчи?
Числа Фибоначчи являются элементами числовой последовательности, где каждое последующее число образуется посредством суммирования двух предыдущих, например: 0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89… Как правило, записывается такая последовательность формулой: F0 = 0, F1 = 1, Fn = Fn-1 + Fn-2, n ≥ 2.
Числа Фибоначчи могут начинаться и с отрицательных значений «n», но в таком случае последовательность будет двусторонней – она будет охватывать и положительные и отрицательные числа, стремясь к бесконечности в двух направлениях. Примером такой последовательности может послужить: -34, -21, -13, -8, -5, -3, -2, -1, 1, 0, 1, 1, 2, 3, 5, 8, 13, 21, 34, а формула будет: Fn = Fn+1 - Fn+2 или же F-n = (-1)n+1Fn.
Создателем чисел Фибоначчи является один из первых математиков Европы средних веков по имени Леонардо Пизанский, которого, собственно и знают, как Фибоначчи – это прозвище он получил спустя много лет после своей смерти.
При жизни Леонардо Пизанский очень любил математические турниры, по причине чего в своих работах («Liber abaci» /«Книга абака», 1202; «Practica geometriae»/«Практика геометрии», 1220, «Flos»/«Цветок», 1225 год – исследование на тему кубических уравнений и «Liber quadratorum»/«Книга квадратов», 1225 – задачи о неопределенных квадратных уравнениях) очень часто разбирал всевозможные математические задачи.
О жизненном пути самого Фибоначчи известно крайне мало. Но достоверно известно то, что его задачи пользовались огромнейшей популярностью в математических кругах в последующие века. Одну из таких мы и рассмотрим далее.
Задача Фибоначчи с кроликами
Для выполнения задачи автором были поставлены следующие условия: есть пара новорождённых крольчат (самка и самец), отличающихся интересной особенностью – со второго месяца жизни они производят новую пару кроликов – тоже самку и самца. Кролики находятся в замкнутом пространстве и постоянно размножаются. И ни один кролик не умирает.
Задача: определить количество кроликов через год.
Решение:
У нас есть:
- Одна пара кроликов в начале первого месяца, которая спаривается в конце месяца
- Две пары кроликов во втором месяце (первая пара и потомство)
- Три пары кроликов в третьем месяце (первая пара, потомство первой пары с прошлого месяца и новое потомство)
- Пять пар кроликов в четвёртом месяце (первая пара, первое и второе потомство первой пары, третье потомство первой пары и первое потомство второй пары)
Количество кроликов в месяц «n» = количеству кроликов прошлого месяца + количество новых пар кроликов, другими словами, вышеназванная формула: Fn = Fn-1 + Fn-2. Отсюда получается рекуррентная числовая последовательность (о рекурсии мы скажем далее), где каждое новое число соответствует сумме двух предыдущих чисел: 1 месяц: 1 + 1 = 2 2 месяц: 2 + 1 = 3 3 месяц: 3 + 2 = 5 4 месяц: 5 + 3 = 8 5 месяц: 8 + 5 = 13 6 месяц: 13 + 8 = 21 7 месяц: 21 + 13 = 34 8 месяц: 34 + 21 = 55 9 месяц: 55 + 34 = 89 10 месяц: 89 + 55 = 144 11 месяц: 144 + 89 = 233 12 месяц: 233+ 144 = 377
И эта последовательность может продолжаться бесконечно долго, но учитывая, что задачей является узнать количество кроликов по истечении года, получается 377 пар.
Здесь важно также заметить, что одним из свойств чисел Фибоначчи является то, что если сопоставить две последовательные пары, а затем разделить большую на меньшую, то результат будет двигаться по направлению к золотому сечению, о котором мы также скажем ниже.
Пока же предлагаем вам ещё две задачи по числам Фибоначчи:
- Определить квадратное число, о котором известно только, что если отнять от него 5 или прибавить к нему 5, то снова выйдет квадратное число.
- Определить число, делящееся на 7, но при условии, что поделив его на 2, 3, 4, 5 или 6 в остатке будет 1.
Такие задачи не только станут отличным способом развития ума, но и занимательным времяпрепровождением. О том, как решаются эти задачи, вы также можете узнать, поискав информацию в Интернете. Мы же не будем заострять на них внимание, а продолжим наш рассказ.
Что же такое рекурсия и золотое сечение?
Рекурсия
Рекурсия является описанием, определением или изображением какого-либо объекта или процесса, в котором есть сам данный объект или процесс. Иначе говоря, объект или процесс можно назвать частью самого себя.
Рекурсия широко используется не только в математической науке, но также и в информатике, массовой культуре и искусстве. Применимо к числам Фибоначчи, можно сказать, что если число равно «n>2», то «n» = (n-1)+(n-2).
Золотое сечение
Золотое сечение является делением целого на части, соотносящиеся по принципу: большее относится к меньшему аналогично тому, как общая величина относится к большей части.
Впервые о золотом сечении упоминает Евклид (трактат «Начала» прим. 300 лет до н.э.), говоря и построении правильного прямоугольника. Однако более привычное понятие было введено немецким математиком Мартином Омом.
Приблизительно золотое сечение можно представить в качестве пропорционального деления на две разные части, к примеру, на 38% и 68%. Численное же выражение золотого сечения равно примерно 1,6180339887.
На практике золотое сечение используется в архитектуре, изобразительном искусстве (посмотрите работы Леонардо да Винчи), кино и других направлениях. На протяжении долгого времени, впрочем, как и сейчас, золотое сечение считалось эстетической пропорцией, хотя большинством людей оно воспринимается непропорциональным – вытянутым.
Вы можете попробовать оценить золотое сечение сами, руководствуясь следующими пропорциями:
- Длина отрезка a = 0,618
- Длина отрезка b= 0,382
- Длина отрезка c = 1
- Соотношение c и a = 1,618
- Соотношение c и b = 2,618
Теперь же применим золотое сечение к числам Фибоначчи: берём два соседних члена его последовательности и делим большее на меньшее. Получаем примерно 1,618. Если же возьмём то же самое большее число и поделим его на следующее большее за ним, то получим примерно 0,618. Попробуйте сами: «поиграйте» с числами 21 и 34 или какими-то другими. Если же провести этот опыт с первыми числами последовательности Фибоначчи, то такого результата уже не будет, т.к. золотое сечение «не работает» в начале последовательности. Кстати, чтобы определить все числа Фибоначчи, нужно знать всего лишь три первых последовательных числа.
И в заключение ещё немного пищи для ума.
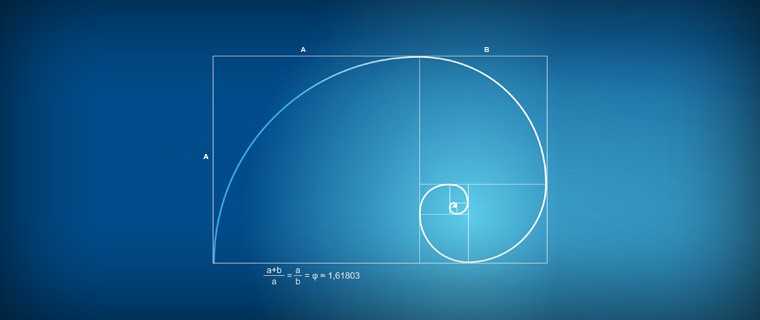
Золотой прямоугольник и спираль Фибоначчи
«Золотой прямоугольник» - это ещё одна взаимосвязь между золотым сечением и числами Фибоначчи, т.к. соотношение его сторон равно 1,618 к 1 (вспоминайте число 1,618!).Вот пример: берём два числа из последовательности Фибоначчи, например 8 и 13, и чертим прямоугольник с шириной 8 см и длинной 13 см. Далее разбиваем основной прямоугольник на мелкие, но их длина и ширина должна соответствовать числам Фибоначчи – длина одной грани большого прямоугольника должна равняться двум длинам грани меньшего.
После этого соединяем плавной линией углы всех имеющихся у нас прямоугольников и получаем частный случай логарифмической спирали – спираль Фибоначчи. Её основными свойствами являются отсутствие границ и изменение форм. Такую спираль можно часто встретить в природе: самыми яркими примерами являются раковины моллюсков, циклоны на изображениях со спутника и даже ряд галактик. Но более интересно то, что этому же правилу подчиняется и ДНК живых организмов, ведь вы помните, что оно имеет спиралевидную форму?
Эти и многие другие «случайные» совпадения даже сегодня будоражат сознание учёных и наводят на мысль о том, что всё во Вселенной подчинено единому алгоритму, причём, именно математическому. И эта наука кроет в себе огромное количество совсем нескучных тайн и загадок.