На сайте мы уже много раз говорили о самых разных видах мышления, но вот именно математическое мышление было незаслуженно обделено вниманием. Наконец-таки мы исправим это упущение. Однако у вас может возникнуть вопрос: «А зачем мне вообще это математическое мышление?». Поэтому сначала вкратце объясним, что это такое, и почему важно уметь думать, как математик.
Что такое математическое мышление и в чем его польза?
Определение математического мышления таково: математическое мышление – это абстрактное теоретическое мышление, объекты которого лишены вещественности, но при этом они могут быть интерпретированы любым произвольным образом с одним лишь условием – должны сохраняться заданные между объектами отношения.
Учитывая то, что математика – это наука не только об уравнениях и формулах, но и о структурах, порядке и отношениях, главное отличие математического мышления от обычного (повседневного) состоит в том, что оно прививает и развивает у человека навык критического восприятия окружающего мира, желание и умение «копнуть глубже» и найти истину, понять причины и суть самых разных понятий и явлений.
Если говорить о практической пользе математического мышления, то в первую очередь (ведь об этом говорит само его определение) на ум приходит, конечно, то, что оно помогает нам справляться с математическими задачами. Однако истинная его ценность намного больше.
Человек, у которого развито математическое мышление:
- Понимает, что у любой проблемы есть решение
- Умеет раскладывать поиск решений проблем на последовательные этапы
- Воспринимает неудачи и ошибки не как причину опускать руки, а как возможность развиваться
Если говорить конкретнее, то умение мыслить, как математик, способствует успехам в учебе, ведь человек привыкает разбивать сложные задачи на более мелкие, удерживать в голове большое количество информации и оперировать ей, справляться с трудностями, выявлять взаимосвязи. Причем все это может пригодиться как в математике, так и в любой другой науке.
Математически мыслящий человек обладает навыком критической оценки информации, ведь окружающая действительность воспринимается им с некоторой долей здорового скептицизма. Это помогает различать правду и вымысел, опираться на факты и доказательства, а не слепо верить тому, что говорят.
Кроме того, математическое мышление помогает в принятии жизненно важных решений. Любая проблема и трудность раскладывается на составляющие, во внимание берутся все вероятные исходы и последствия. А благодаря уверенности в решаемости любых проблем человек охотнее берет на себя ответственность, менее подвержен страхам и сомнениям, может в любой ситуации придумать план действий.
Еще один полезный аспект развитого математического мышления состоит в том, что оно помогает преодолеть злосчастную привычку откладывать дела на потом, нерешительность перед сложными задачами. А все это вместе взятое служит тем самым стержнем, на котором держатся все составляющие успешной, образованной, уверенной в себе и самостоятельной личности. И это самым прямым образом влияет на достигаемые человеком в жизни и работе результаты.
Посмотрите это видео, в котором математик Эдуардо Саенц де Кабезон на конференции TED в остроумной манере рассказывает о пользе математики в жизни. [embed width="100%"]https://www.youtube.com/watch?v=4QHUnxmd1WE[/embed]
Таким образом, математическое мышление является навыком, необходимым каждому, кто стремится к достижению высоких целей. Но перед тем как начинать развивать его, необходимо хотя бы в общих чертах понять его природу.
Особенности математического мышления
Ученые уже не один десяток лет пытаются понять, откуда вообще в человеке есть способность к проведению математических вычислений. Для объяснения этого феномена предложены две теории. Смысл первой сводится к тому, что склонность к математике – это побочный эффект появления речи и языка. А вторая говорит, что причиной всему возможность применения интуитивного понимания пространства и времени, причем корни этого понимания тянутся вглубь веков.
Пытаясь понять, какая же теория верна, психологи провели эксперимент, для которого взяли 15 обычных людей и 15 математиков с одним и тем же уровнем образования. Обеим группам предлагали несколько сложных математических и нематематических утверждений, и участники должны были оценить их истинность, ложность или бессмысленность. Во время эксперимента мозг каждого испытуемого сканировался томографом.
В результате выяснилось, что заявления, касавшиеся математических областей (геометрии, алгебры, топологии, анализа и т.д.), возбуждали участки префронтальной, нижневисочной и теменной коры головного мозга только у математиков, но не у второй группы испытуемых. И эти зоны отличались от тех, что активизировались у каждого испытуемого при обработке нематематических утверждений. Вышеназванные зоны «работали» у обычных людей только тогда, когда они решали простейшие арифметические задачи.
С научной точки зрения этот результат объясняется тем, что математическое мышление более высоких уровней задействует нейронную сеть, отвечающую за восприятие времени, пространства и чисел. И эта нейронная сеть отличается от той, что связана с языком. Это приводит нас к выводу, что на развитие математического мышления непосредственно влияет развитие пространственного мышления. Кстати, чтобы понять, как математика взаимодействует с психологией и другими науками, можете почитать книгу «Математическое мышление» выдающегося немецкого математика и физика-теоретика Германа Вейля.
Еще одна особенность математического мышления состоит в том, что в его структуре выделяются несколько пересекающихся подструктур, называемых типами математического мышления (эта идея была предложена кандидатом психологических наук Ильей Яковлевичем Каплуновичем). От того, какой из этих типов доминирует, зависит мыслительная деятельность человека в любой практической ситуации.
Типы математического мышления
Всего можно выделить пять типов математического мышления. Расскажем о них в тезисной форме:
- Топологическое мышление. Его развитие у детей происходит раньше всех остальных – в возрасте 2-3 лет. От него зависит связанность и целостность логических операций. Люди с этим типом мышления действуют не наобум, а сначала улавливают нить и изучают детали, и только потом не спеша и тщательно доводят дело до конца. Качества, присущие людям-топологам: аккуратность, размеренность, консервативность, медлительность и дотошность.
- Порядковое мышление. Развивается у человека вслед за топологическим. От него зависит точная последовательность логических операций. Люди с преобладающим порядковым мышлением не обязательно объединяют действия в единое целое, но всегда придерживаются строгого линейного порядка и следуют от начального к конечному. В работе придают больше значение размеру и форме объектов и их соотношению, четко следуют плану, вырабатывают конкретный алгоритм. Качества таких людей: педантичность, соблюдение общепринятых правил, следование инструкциям.
- Метрическое мышление. Развивается, как и все остальные типы, после первых двух. Отвечает за количественные запросы и оперирует цифрами. Люди-метристы все сводят к конкретным величинам, руководствуются точными параметрами, не очень любят общность и образность, т.к. для них трудно представлять абстрактные и неопределенные величины. Зато они всегда точно знают, к каким результатам приведут их действия, и каких усилий это будет им стоить. Качества людей с доминирующим метрическим мышлением: предусмотрительность и осторожность, желание просчитать все наперед, узнать все нюансы и подробности.
- Алгебраическое мышление. Присуще комбинаторам и конструкторам. Люди с преобладающим алгебраическим мышлением обладают структурным восприятием и выстраивают комбинации; работу могут начинать с любого места, и перескакивать в процессе с одного на другое. Не любят общепринятых правил и рамок. Качества таких людей: некоторая рассеянность, непунктуальность, упрощение всего сложного, способность быстро выделять главное.
- Проективное мышление. Многие считают его самым важным из всех. Людей с таким мышлением отличает умение смотреть на вещи с разных сторон, интерес к множеству вариантов действий, нестандартность в решениях. Другие качества этих людей: неординарный интеллект, стремление к выгоде во всем, лидерские качества, способность к быстрой оценке ситуаций, невнимательность к абсолютным характеристикам и важным деталям.
Эти типы математического мышления развиты в каждом человеке в разных пропорциях. У большинства людей преобладает порядковое мышление, причиной чему служит, помимо прочего, стандартная система школьного образования, работающая именно по порядковой схеме.
Определить свой преобладающий тип математического мышления можно при помощи специализированных тестов, которые можно найти в Интернете. Но можно и просто понаблюдать за своими повседневными действиями. Попробуйте, например, описать свою комнату, перечислить все, что в ней есть, а затем оцените свой ответ:
- С преобладающим топологическим мышлением вы перечислите все предметы в комнате по группам
- С преобладающим порядковым мышлением вы расскажете о размерах и формах предметов, их расположении относительно друг друга
- С преобладающим метрическим мышлением вы назовете габариты помещения и количество тех или иных предметов
- С преобладающим алгебраическим мышлением вы просто будете перечислять все подряд, перескакивая с одного на другое
- С преобладающим проективным мышлением вы не просто вспомните все, что есть комнате, но и посвятите слушателя в особенности применения тех или иных объектов
И еще один интересный факт: люди, у которых преобладает один и тот же тип мышления, неосознанно тянутся друг к другу, т.к. им часто сложно понять систему мышления тех, кто от них отличается. Но давайте отойдем от типологии и теории, и уделим внимание основной теме нашей статьи и практической части.
Основываясь на результатах эксперимента, о котором мы рассказывали выше, можно сделать вывод о том, как развить математическое мышление: нужно развивать мышление пространственное. И сейчас мы расскажем о том, как это делается (а в конце статьи предложим несколько рекомендаций по развитию математического мышления вне зависимости от пространственного).
Пространственное мышление: определение и развитие

Пространственное мышление необходимо нам для решения множества задач, которые ставит жизнь. Речь здесь в первую очередь идет о пространственном воображении – способности детализировано представлять трехмерные объекты. С помощью нее мы можем манипулировать любой воображаемой или реальной пространственной структурой, оценивать ее пространственные отношения и свойства, видоизменять ее и создавать новые структуры.
Пространственное мышление является совершенно особым видом деятельности, имеющим огромное значение для решения задач, которые ставят нас перед необходимостью ориентироваться в теоретическом или практическом пространстве. В наиболее развитой форме пространственное мышление – это мышление при помощи образов, в которых фиксируются пространственные отношения и свойства.
Психология уже давно говорит о том, что зачатки пространственного мышления присутствуют с рождения у ничтожно малого количества людей, а потому оно нуждается в развитии. Заниматься этим полезно любому человеку и в любом возрасте. И важно это не только потому, что развивается математическое мышление, но и потому, что такая деятельность обеспечивает нормальное функционирование мозга, служит профилактикой множества заболеваний, вызываемых дефицитом работы нейронов.
Если затронуть конкретно развитие у детей, то пространственное мышление повышает успехи в освоении технических наук и даже изучении литературы, ведь оно позволяет создавать в сознании целые динамические картины, основанные на прочитанных текстах. Соответственно, ребенку становится легче анализировать художественные произведения; повышается интерес к чтению. Ну а о том, что пространственное мышление пригодится на любимых детьми уроках труда и рисования, пожалуй, и говорить не стоит.
Несмотря на то, что в той или иной степени пространственное мышление развивается в человеке с детских лет, уже к подростковому возрасту это развитие останавливается. Но при желании можно самостоятельно его развивать и совершенствовать. Для этого используются специальные упражнения (их можно применять для развития у детей и у взрослых).
Упражнение «Представление»
Задача – просто представлять какие-то объекты. Проще всего – линии и отрезки. Вот несколько примеров:
- Представьте две сближающиеся линии. Определите место их пересечения.
- Представьте треугольник, наложенный на две линии. Что вы видите?
- Представьте три разнонаправленных линии. Мысленно соедините их и нарисуйте полученный объект.
Упражнение «Угадывание на ощупь»
Возьмите помощника. Закройте глаза и попросите его дать вам в руки какой-нибудь предмет, к примеру, фрукт, ткань, детскую игрушку, пульт от телевизора и т.д. На изучение объекта дается от 15 до 90 секунд (в зависимости от возраста и степени развития пространственного мышления). Отдайте предмет напарнику и скажите, что было у вас в руках.
Упражнение «Копирование»
Задания в этом упражнении постепенно усложняются. Алгоритм такой:
- Смотрите на какой-нибудь объект (желательно, чтобы он мог поместиться на листе формата А4) и перечерчивайте его на бумагу в реальном размере.
- Скопируйте тот же самый объект, но добавьте к нему 5 см в длине и какой-нибудь дополнительный элемент.
- Скопируйте любой небольшой объект на бумагу, увеличив его в 3 раза, уменьшив в 4 раза и т.п.
- Представьте какую-нибудь объемную фигуру и нарисуйте ее с разных сторон.
Упражнение «Муха в клетке»
Для начала найдите себе двух помощников. Двое из вас будут выполнять задание, а третий будет следить за игрой и проверять результаты.
Суть упражнения: вместе со своим помощником представьте решетку 9х9 квадратов (у третьего участника должна быть ее графическая схема, но вам ей пользоваться нельзя). В ее правом верхнем углу сидит муха. Определите очередность ходов и по очереди перемещайте муху по квадратам. Обозначайте движения и число клеток.
Например, вы передвигаете муху на 4 клетки вниз. Наблюдающий обозначает ваш ход на своей схеме. Так же он действует с каждым другим ходом. В какой-то момент он говорит: «Стоп», а вы со своим напарником должны сказать, в каком конкретно квадрате находится муха.
Победителем будет тот, кто даст правильный ответ (его должен подтвердить наблюдающий). Кстати, если хотите усложнить игру, можете изменить количество клеток решетки (она не обязательно должна быть симметричной).
В дополнение к этим упражнениям можно использовать и другие методы.
Схемы и чертежи
Опираясь на какой-то наглядный материал (или без него), например, на предметы в своей комнате, составляйте их планы, схемы и чертежи. Если взять комнату, то в ее плане должны присутствовать все предметы и их схемы. С тем же успехом можно рисовать чертежи зданий, магазинов, автомобилей и т.д.
Оригами и 3D-паззлы
Поищите в Интернете самоучители по оригами и учитесь складывать из бумаги различные фигурки. Также для этого подходят 3D-паззлы, которые можно купить в любом книжном магазине.
В начале работы представляйте желаемые фигуры и старайтесь определять необходимый порядок действий. Задания лучше всего усложнять:
- Повторять действия за кем-то
- Действовать про инструкции
- Действовать, изредка подглядывая в инструкцию
- Создавать фигуры самостоятельно
Графические тренажеры
Сегодня есть множество графических тренажеров, созданных специально для развития пространственного мышления. В качестве примера мы взяли несколько изображений из книги известного детского педагога Израиля Зиновьевича Постоловского «Тренировка образного мышления».
Вот такими могут быть задания:
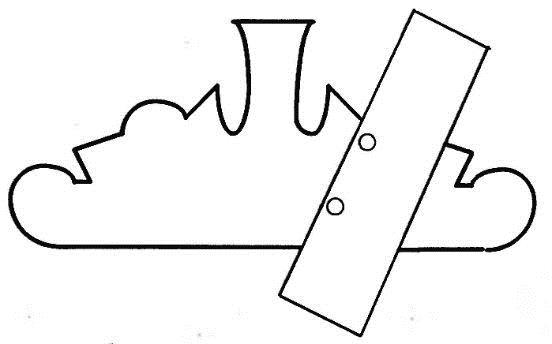
- Восстановите закрытый линейкой элемент фигуры
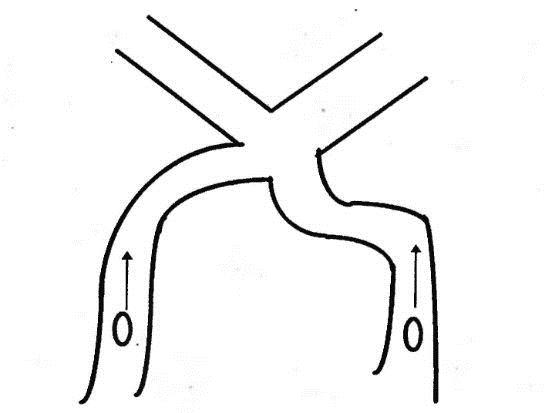
- Представьте, что овалы на рисунке – это машины. Какая быстрее доедет до перекрестка при равной скорости?
- Куда упадет шарик на картинке ниже?

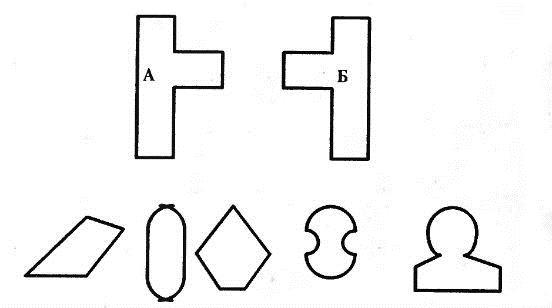
- Сколько фигур смогут «пройти» между объектами А и Б, и какие именно?
- На какой отметке должен оказаться человек, чтобы на него не упало дерево?

Это всего лишь несколько способов, как развить пространственное мышление, и при желании в Интернете можно найти немалое количество других упражнений и игр.
Теперь же давайте немного отстранимся от пространственного мышления и вернемся к математическому. Ниже мы приводим несколько рекомендаций по его развитию у детей и у взрослых.
Рекомендации по развитию математического мышления
Для развития математического мышления полезно заниматься развитием логики и как можно больше работать с цифрами. В первую очередь при необходимости любых вычислений в повседневной жизни старайтесь производить их в уме – без использования калькулятора.
Учитывая склонность мозга к тому, чтобы чаще не думать, чем думать, стремитесь активизировать активность интеллекта. Выполняйте специальные задачи и упражнения на логику, играйте в математические игры, решайте головоломки, ребусы и кроссворды, играйте в шахматы, пользуйтесь онлайн-тренажерами и тестами.
Обязательно правильно питайтесь, чтобы в ваш организм поступали все нужные ему витамины, минералы и микроэлементы. Чередуйте умственную деятельность с физическими нагрузками, т.к. физические упражнения позволяют мозгу отдохнуть, а также способствуют выработке организмом полезных гормонов.
А говоря о детском развитии, заметим, что развивать математический склад ума необходимо уже с малых лет. Оптимальным возрастом для начала занятий считается период от 1 до 3 лет, т.к. позже намного удобнее работать с уже частично сформированной у ребенка математической базой и развивать ее, нежели постигать азы.
Чтобы привить ребенку интерес к математике, нужно делать так, чтобы он воспринимал ее не как скучную прикладную науку, а как интересное занятие. Для этого полезно как можно чаще задавать разные задачки, использовать игрушки, считалки, активные игры на математическую тему, демонстрировать наглядные примеры простейших математических вычислений и их полезность. Правильное питание и физические нагрузки относятся и к детям тоже, причем даже больше, чем к взрослым.
Помимо прочего, предлагаем вам почитать наши статьи «Как объяснить ребенку математику?» и «Уроки математики для малышей», а также книгу «Как обучить вашего малыша математике» Гленна и Джанет Доман. А для вашей личной пользы советуем почитать книги «Математическое мышление» (Герман Вейль) и «Думай как математик» (Барбара Оакли) и посмотреть видео от российского математика и физика Алексея Семихатова о связи математики и интуиции. [embed width="100%"]https://www.youtube.com/watch?v=l8tGfLcn3i0[/embed]
Желаем вам удачи в обучении, и пусть математическое мышление помогает вам не только решать примеры, но и добиваться успехов в жизни!