Урок 4. Суждения и высказывания. Введение в силлогистику
 В прошлых уроках рассказывалось о том, как правильно работать с понятиями и определениями. Хотя операции над ними очень важны и встречаются повсеместно, сами по себе они ещё не составляют рассуждений.
В прошлых уроках рассказывалось о том, как правильно работать с понятиями и определениями. Хотя операции над ними очень важны и встречаются повсеместно, сами по себе они ещё не составляют рассуждений.
В этом уроке мы как раз приблизимся к теме того, как правильно рассуждать. Мы будем рассматривать рассуждения на примере силлогистики.
Силлогистика – это самая древняя логическая система. Она была изобретена древнегреческим философом Аристотелем в IVвеке до н.э. До сих пор она остаётся одной из самых понятных, приближенных к естественному языку и лёгких для изучения логических систем. Одно из главных её достоинств – возможность применения в повседневных ситуациях без особых усилий.
Содержание:
- Суждения и высказывания
- Состав и виды категорических атрибутивных высказываний
- Условия истинности для категорических атрибутивных высказываний в традиционной силлогистике
- Упражнения
- Проверочный тест
Суждения и высказывания
Что такое рассуждение? Можно было бы сказать: вывод, умозаключение, размышление, доказательство и т.д. Всё это верно, но, пожалуй, самым очевидным ответом было бы: рассуждение – это последовательность суждений, которые в идеале должны быть связаны между собой согласно правилам логики. Поэтому обучение правильному рассуждению нужно начинать с того, что такое суждения и как ими корректно пользоваться.
Суждение – это мысль об утверждении или отрицании наличия некоторой ситуации в мире.
В естественном языке суждения передаются с помощью повествовательных предложений, или высказываний. Примеры суждений, выраженных в высказываниях: «Пришла осень», «Катя не знает английского языка», «Я люблю читать», «Трава зелёная, а небо голубое». Одно и то же суждение может быть выражено с помощь разных высказываний, в частности: «Небо голубое» и «The sky is blue» – разные высказывания, но суждение они выражают одно и то же, так как они передают одну и ту же мысль. Точно также высказывания «Никто не покидал дома» и «Все оставались дома» разные, но они передают одно суждение.
Поскольку высказывания посредством суждений фиксируют какое-то положение дел в мире, в отличие от понятий и определений, мы можем оценивать их с точки зрения их истинности и ложности. Так высказывание «Бил Гейтс основал компанию “Microsoft”» – истинное, а высказывание «Апельсины фиолетовые» – ложное.
Если вспомнить треугольник Фреге, то высказывание будет находиться на вершине, обозначающей знак, суждение будет составлять его смысл, а истина и ложь – значение.
Существует множество типов суждений и, соответственно, высказываний. Разные логические системы концентрируются на их разных аспектах. Силлогистика работает с так называемыми категорическими атрибутивными высказываниями. Категорические высказывания противопоставляются гипотетическим. Гипотетические высказывания говорят о возможности наличия или отсутствия какой-то ситуации в мире: «Возможно, пойдёт дождь».
Категорические высказывания безапелляционно утверждают о том, что какая-то ситуация имеется или не имеется: «Пошёл дождь». Термин «атрибутивный» означает, что эти высказывания говорят о наличии либо отсутствии у предмета или класса предметов некоторого свойства.
Примеры категорических атрибутивных высказываний: «Моя машина синего цвета», «Парк около нашего дома большой», «Никто не любит рыбий жир», «Некоторые люди считают, что они самые умные». Хотя на первый взгляд может показаться, что из-за концентрации именно на категорических атрибутивных высказываниях, применение силлогистики ограничено, это не так. Огромный пласт рассуждений не выходит за рамки подобных высказываний, а потому знания силлогистики оказывается достаточно для того, чтобы научиться размышлять логично и не давать ввести себя в заблуждение.
Состав и виды категорических атрибутивных высказываний
Категорические атрибутивные высказывания состоят из терминов, предицирующих связок и кванторов.
Термины делятся на субъект и предикат.
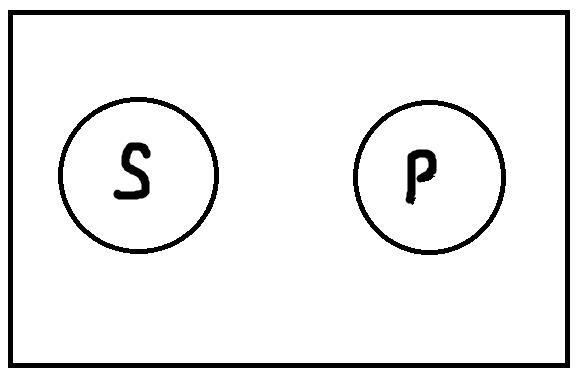
| | Субъект – это термин, обозначающий предмет или группу предметов, о которых нечто утверждается или отрицается. Обычно субъект изображается с помощью буквы S. |
| | Предикат – это термин, обозначающий собственно то, что утверждается или отрицается о субъекте, некоторое свойство, признак, наличие или отсутствие которого приписывается субъекту. Предикат изображается с помощью буквы P. |
Предицирующие связки, как, возможно, вы помните из первого урока, это связки «есть» и «не есть». В естественном языке они могут выражаться с помощью разных слов и конструкций: «есть», «являться», «суть», «это», «выступать», знака тире, глаголов, либо вообще опускаться.
Кванторы – это слова, указывающие на количественные характеристики субъекта. Существует два вида кванторов: квантор общности («все», «каждый», «любой», «ни один», «никто») и квантор существования («некоторые», «не все», «какой-либо», «многие»). Также как и предицирующие связки, кванторы в естественной речи могут опускаться.
Мы можем сказать: «Люди равны перед законом», подразумевая, что «Все люди равны перед законом»; или «Дети любят сладкое» – подразумевая, что «Многие дети любят сладкое». Зачастую лучше всего уточнить у вашего собеседника, какой именно квантор он имеет в виду, так как это будет сказываться на условиях истинности его высказываний.
Давайте разберём следующее высказывание: «Кошки мурлычут, когда им приятно». «Кошки» – это субъект, «существа, мурлычущие, когда им приятно» – это предикат. Также здесь присутствует невидимая связка «есть», которая соединяет субъект с предикатом, и невидимый квантор общности «все».
Так, если записать это высказывание в соответствии с его логической формой, то получим: «Все кошки есть существа, которые мурлычут, когда им приятно». Благодаря этому примеру становится ясно, что прежде чем определять, истинно высказывание или ложно, нужно выявить его логическую форму и преобразовать исходное высказывание так, чтобы все четыре элемента (квантор, субъект, связка, предикат) были на своих местах.
В зависимости от свойств логических и нелогических терминов, входящих в состав категорических атрибутивных высказываний, их можно разделить на несколько видов.
- В зависимости от характера субъекта категорические атрибутивные высказывания делятся на единичные и множественные. Если в качестве субъекта выступает имя, то речь идёт о единичном высказывании («Сократ был философом»). Единичные высказывание не имеют квантора перед субъектом.
- В зависимости от предицирующей связки высказывания делятся на утвердительные и отрицательные. Если утверждается наличие какого-то свойства у субъекта, то высказывание утвердительное («Петя – настоящий друг»), если отрицается – то отрицательное («Ни один студент не пришёл на первую пару!»).
Если мы скомбинируем эти виды между собой, то получается, что всего существует шесть видов категорических атрибутивных высказываний:
- Единичноутвердительные: s есть P. Александр Пушкин – это русский писатель.
- Единичноотрицательные: s не есть P. Сервантес не был художником.
- Общеутвердительные: Все S есть P. Все квартиры в этом доме имеют высокие потолки.
- Общеотрицательные: Ни один S не есть P. Ни один студент из нашей группы не сдал экзамен на пятёрку.
- Частноутвердительные: Некоторые S есть P. Некоторые машины из нашего автопарка нуждаются в срочном ремонте.
- Частноотрицательные: Некоторые S не есть P. Некоторые тексты песен не имеют смысла.
Условия истинности для категорических атрибутивных высказываний в традиционной силлогистике
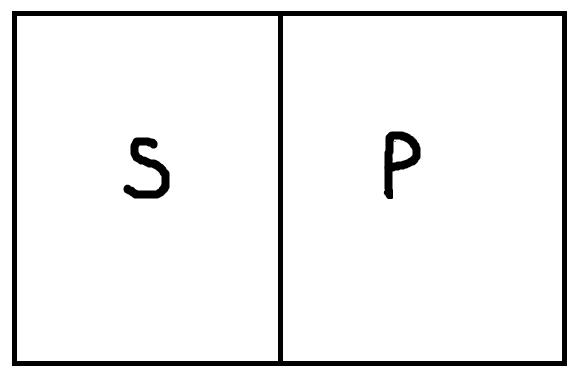
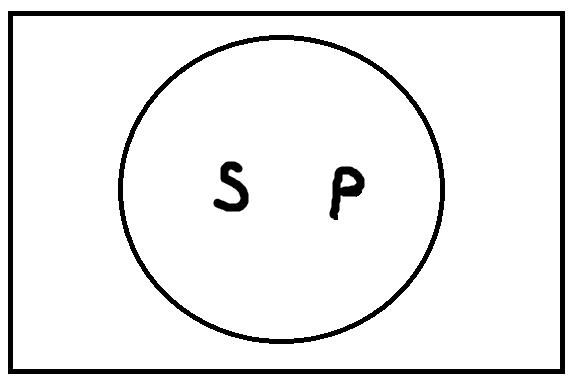
Следует начать с того, что традиционная силлогистика накладывает два ограничения на используемые термины, а именно: они должны быть непусты и неуниверсальны, то есть если под термин не подпадает ни один объект из универсума рассмотрения или, наоборот, подпадают все объекты универсума, то они не могут быть предметом рассмотрения. Посмотрим на рисунки:
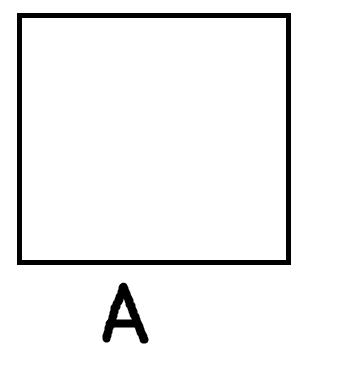
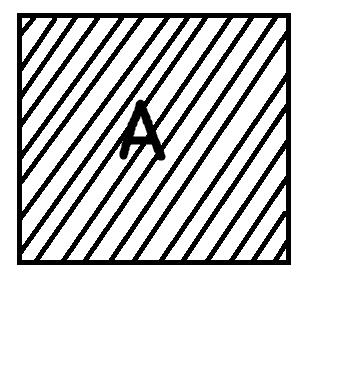
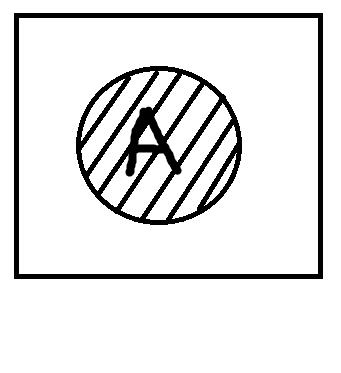
Первый рисунок изображает ситуацию, когда термин А пуст, поэтому весь квадратик (универсум рассмотрения) остался белым. Второй рисунок показывает случай, когда объём термина А совпадает с объёмом универсума рассмотрения, поэтому весь квадрат заштрихован. Последний рисунок репрезентирует термин А, который является непустым и в то же время неуниверсальным. Заштрихованая область соотвествует объёму А. Традиционная силлогистика работает только с терминами, которые соотвествуют третьему рисунку.
Такое условие ставится для того, чтобы исключить из рассмотрения высказывания, которые невозможно оценить как истинные либо ложные. Возьмём высказывание: «Все дети Ивана лысые». Вроде бы с высказыванием всё впорядке, однако представьте, что у Ивана нет детей. Мы не можем в данном случае просто сказать, что высказывание ложное. Если назвать его ложным, то тем самым мы подразумеваем, что не все дети Ивана лысые, а это не так. В то же время мы не можем сказать, что оно истинное. Выход из этого затруднительного положения состоит как раз в том, чтобы указать на пустоту термина «дети Ивана». Поскольку у Ивана нет детей, этот термин пуст, и мы не можем построить с ним корректное высказывание.
То же самое верно и для универсальности. Термин «люди» может рассматриваться как универсальный, что исключает его из области традиционной силлогистики. Однако если мы хотим сказать «Сократ – человек», то в качестве универсума рассмотрения вполне можно взять живых существ. На универсуме живых существ, термин «люди» уже не будет универсальным.
Кроме того, нужно помнить, что субъект и предикат должны задаваться на одном и том же универсуме рассмотрения.
Теперь посмотрим, при каких условиях разные типы категориальных атрибутивных высказываний будут истинными. Для этого советуем ещё раз заглянуть в урок, посвящённый отношениям между понятиями. По большому счёту, субъект и предикат – это термины, представляющие некоторые понятия. Соответственно, если соединить эти понятия в одном предложении с помощью предицирующих связок и кванторов, то, чтобы узнать будут эти предложения истинными или ложными, достаточно посмотреть на диаграммы, иллюстрирующие отношения между этими двумя понятиями. Итак, преступим.
Единичноутвердительные высказывания формы «s есть P» истинны, только если термины s и P находятся в следующем отношении:
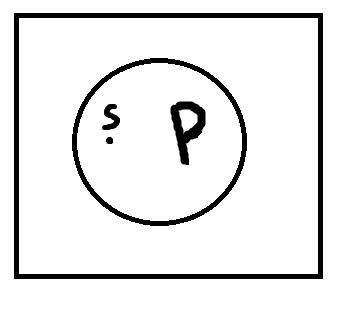
Другими словами, единичноутвердительные высказывания истинны, если точка, представляющая собой имя s, находится внутри кружочка, изображающего объём термина P. Например, возьмём высказывание «Лев Толстой проповедовал вегетарианство». «Лев Толстой» – это субъект, имя s. «Человек, проповедующий вегетарианство» – это предикат, термин P. Это высказывание истинно, так как точка s будет входить в объём термина P. Если же взять высказывание «Николай Гоголь – это великий русский композитор», то точка s, представляющая имя («Николай Гоголь»), не будет входить в объём термина P («великие русские композиторы»). Поэтому это высказывание ложно.
Единичноотрицательные высказывания, имеющие форму «s не есть P» истинны, если термины s и P находятся в следующем отношении:
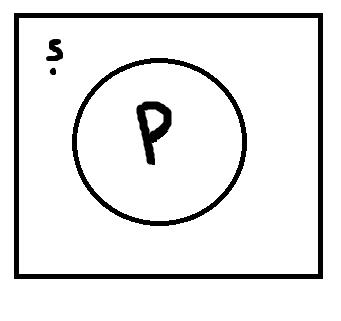
Как видно из рисунка, здесь имеет место ситуация, прямо противоположная условиям истинности единичноутвердительных высказываний. Если точка, представляющая имя s, находится вне объёма термина P, то высказывание истинно. В обратном случае, оно ложно. Пример истинного единичноотрицательного высказывания: «Александр Пушкин никогда не был во Франции». Ложным единичноотрицательным высказыванием будет: «Иван Бунин не получил Нобелевскую премию по литературе».
Общеутвердительные высказывания формы «Все S есть P» истинны, если термины S и P находятся в одном из следующих отношений:
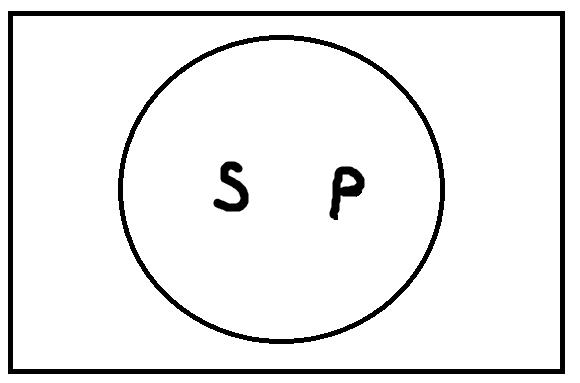
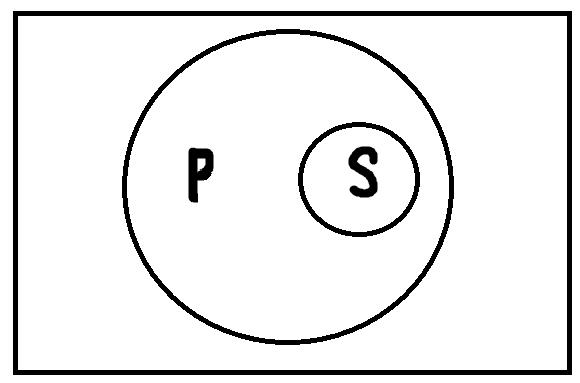
Первый рисунок изображает отношение равнообъёмности, второй – обратного подчинения. Если объёмы двух терминов совпадают (S и P делят один кружочек) или объём термина S полностью входит в объём термина P (кружочек S полностью включается в P), то общеутвердительное высказывание истинно. Если термины S и P находятся в каком-либо другом отношении, то общеутвердительные высказывания не могут быть истинными. В качестве иллюстрации истинных высказываний можно привести: «Все хвойные растения имеют шишки», «Все киты – это млекопитающие». Пример ложных высказываний: «Все политики – обманщики», «Все девушки мечтают выйти замуж за миллионера». В этих примерах термины, обозначающие субъект и предикат, не находятся ни в одном из указанных выше отношений.
Общеотрицательные высказывания, имеющие форму «Ни один S не есть P» истинны, только если термины S и P находятся в следующих отношениях:
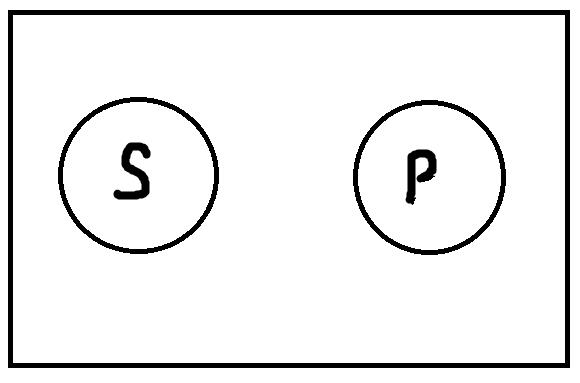
На первом рисунке представлено отношение противоречия, а на втором – соподчинения. Как видно, у S и P нет общих элементов, их объёмы не пересекаются. К примеру, истинными будут высказывания: «Ни один павлин не относится к числу певчих птиц», «Ни один человек младше восемнадцати лет не является совершеннолетним в России». Пример ложного высказывания: «Ни один гуманитарий не разбирается в математике». Высказывание ложно, так как термины «гуманитарий» и «люди, разбирающиеся в математике» не находятся ни в отношении противоречия, ни в отношении соподчинения.
Частноутвердительные высказывания формы «Некоторые S есть P» истинны, если термины S и P находятся в следующих отношениях:
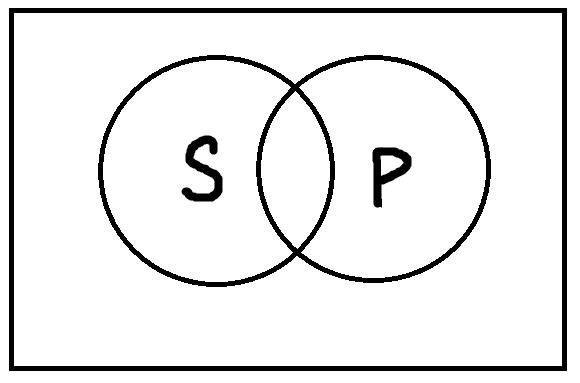

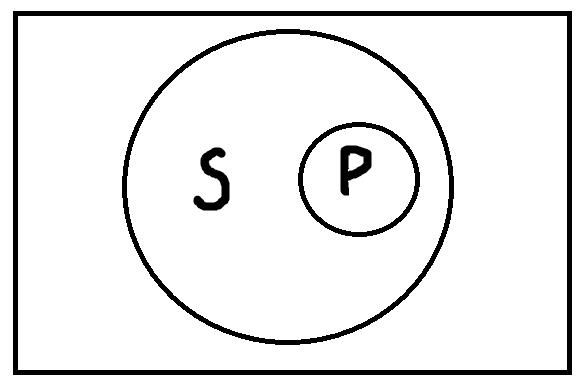
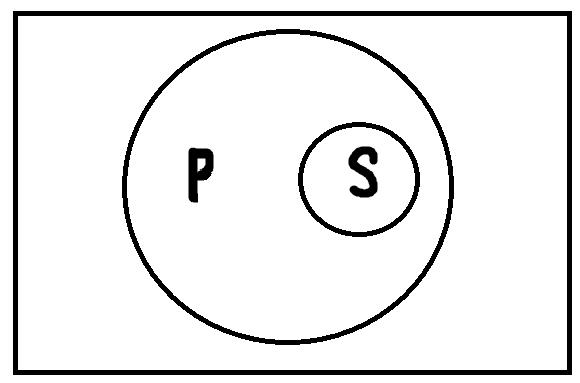
Рисунки последовательно представляют отношения: пересечения, дополнительности, подчинения, равнообъёмности и обратного подчинения. С первыми тремя картинками всё должно быть довольно ясно: видно, что объёмы терминов S и P пересекаются, поэтому в области пересечения находятся элементы, которые одновременно обладают и признаком S и признаком P. Примеры истинных высказываний таких типов: «Некоторые актёры хорошо поют», «Некоторые автомобили с ценой ниже миллиона стоят больше шестисот тысяч», «Некоторые грибы съедобны».
Что касается отношений равнообъёмности и обратного подчинения, то может возникнуть вопрос, почему они тоже представляют собой условия истинности для частноутвердительных высказываний, если на картинках, обозначающих их, чётко видно, что не только некоторые S есть P, но все S есть P. Правда, естественный язык толкает нас к идее, что если некоторые S есть P, то ещё существуют и другие S, которые не есть P: некоторые грибы съедобны, а некоторые несъедобны.
Для логиков такое заключение неверно. Из высказывания «Некоторые S есть P» нельзя вывести заключение, что некоторые S не есть P. Зато из высказывания «Все S есть P» можно заключить, что и некоторые S есть P, потому что если что-то верно относительно всех элементов объёма термина, то оно будет верно и относительно некоторых отдельных элементов. Поэтому в силлогистике слово «некоторые» употребляется в значении «по крайней мере некоторые», но не в значении «только некоторые». Таким образом, из высказывания «Все папоротники размножаются спорами» можно смело вывести и высказывание «Некоторые папоротники размножаются спорами», а из высказывания «Все ученики пятого класса являются пионерами» – высказывание «Некоторые ученики пятого класса являются пионерами».
Частноутвердительные высказывания будут ложными, только если термины S и P находятся в отношении противоречия или соподчинения: «Некоторые тракторы – это самолёты», «Некоторые ложные высказывания истинны».
Частноотрицательные высказывания типа «Некоторые S не есть P» истинны, если термины S и P находятся в следующих отношениях:
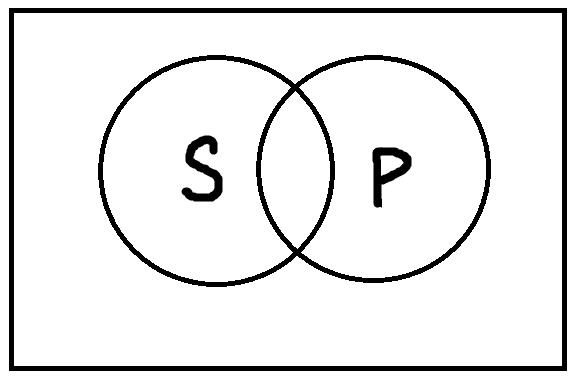

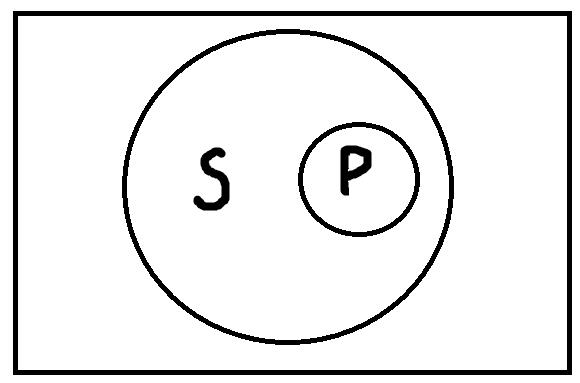
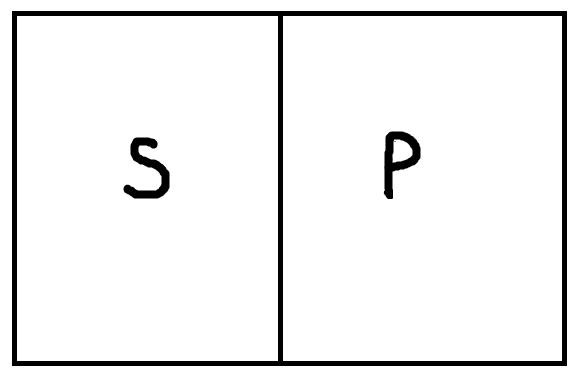
Это отношения: пересечения, дополнительности, включения, противоречия и соподчинения. Очевидно, что первые три отношения совпадают с тем, что было верно и для частноутвердительных высказываний. Все они как раз представляют случаи, когда некоторые S есть P, и в то же время некоторые S не есть P. Примеры подобных истинных высказываний: «Некоторые здоровые люди не употребляют алкоголь», «Некоторые наши работники из категории младше сорока ещё не достигли возраста и двадцати пяти», «Некоторые деревья не являются вечнозелёными».
По тем же причинам, по которым отношения равнообъёмности и обратного подчинения представляли собой условия истинности для частноутвердительных высказываний, отношения противоречия и соподчинения будут верны для частноотрицательных высказываний. Из высказывания, имеющего форму «Некоторые S не есть P» нельзя логично вывести высказывание «Некоторые S есть P». Однако из высказывания «Все S не есть P» можно перейти к высказыванию «Некоторые S не есть P», так как на основании информации, которой мы обладаем обо всех элементах объёмов терминов S и P, можно сделать вывод и об их отдельных представителях. Поэтому верными будут высказывания: «Некоторые журналы не являются книгами», «Некоторые глупцы не являются умными» и т.п.
Итак, мы выяснили, при каких условиях высказывания той или иной формы будут истинными и ложными. При этом стало понятно, что не всегда истинность и ложность высказываний с логической точки зрения совпадает с нашими интуитивными представлениями. Иногда одинаковые на первый взгляд высказывания оцениваются совершенно по-разному, так как за ними скрываются разные логические формы и, следовательно, разные отношения между входящими в них терминами. Эти условия истинности важно запомнить. Они пригодятся, когда в следующем уроке мы научимся складывать высказывания в цепочки рассуждений и будем пытаться найти такие формы умозаключений, которые будут всегда правильными.
Упражнения
Сначала вам предстоит сыграть в интересную игру.
Игра "Пересечение множеств"
В этом упражнении вам нужно внимательно прочитать текст задания и правильно расположить множества, соответствующие понятиям.
А сейчас небольшая работа с высказываниями.
Работа с высказываниями
Прочитайте следующие категориальные атрибутивные высказывания. Определите, к какому типу они относятся. С помощью диаграмм покажите, истинны они или ложны.
- Всё действительное разумно, всё разумное действительно.
- Соль – это яд.
- Яд – это соль.
- Все музыканты имеют хороший слух.
- Некоторые музыканты имеют хороший слух.
- Все люди, имеющие хороший слух, – музыканты.
- Некоторые люди, имеющие хороший слух, – музыканты.
- Некоторые вампиры опоздали на работу.
- Волколаки – это разновидность оборотней.
- Все круглые квадраты не имеют углов.
- Никто не любит, когда у него болят зубы.
- Ни один попугайчик не пьёт виски.
- Некоторым не нравится их работа.
- Иван Иванович поссорился с Иваном Никифоровичем.
- Фильмы Тарковского считаются классикой русского кино.
- Достоевский никогда не играл в карты.
- Некоторые куздры совсем не глокие.
- Каждый сотрудник мечтает о повышении.
- Некоторые псы умеют читать.
- Все счастливые семьи похожи друг на друга, каждая несчастливая семья несчастлива по-своему.
- Некоторые акулы – это рыбы.
- Некоторые люди не летали на Марс.
Теперь давайте закрепим материал урока с помощью теста.
Проверьте свои знания
Если вы хотите проверить свои знания по теме данного урока, можете пройти небольшой тест, состоящий из нескольких вопросов. В каждом вопросе правильным может быть только один вариант. После выбора вами одного из вариантов система автоматически переходит к следующему вопросу. На получаемые вами баллы влияет правильность ваших ответов и затраченное на прохождение время. Обратите внимание, что вопросы каждый раз разные, а варианты перемешиваются.
Далее побеседуем на тему законов и противоречий.

 Ксения Галанина
Ксения Галанина