Урок 2. Понятие в логике
 Скорее всего, немногие люди задумываются над тем, что они мыслят и рассуждают с помощью понятий. Понятия подобны воздуху: мы их не замечаем, но при этом не можем без них размышлять. Каждый ребёнок естественно научается думать с их помощью в семь-восемь лет, переходя от оперирования с конкретными предметами к оперированию с идеями.
Скорее всего, немногие люди задумываются над тем, что они мыслят и рассуждают с помощью понятий. Понятия подобны воздуху: мы их не замечаем, но при этом не можем без них размышлять. Каждый ребёнок естественно научается думать с их помощью в семь-восемь лет, переходя от оперирования с конкретными предметами к оперированию с идеями.
Тем не менее, это не означает, что каждый умеет правильно ими пользоваться, а ведь без этого умения путь к логичному рассуждению закрыт.
Вот почему в этом уроке, мы расскажем, что такое понятия, какие бывают виды понятий, как разные понятия соотносятся друг с другом и как с ними правильно обращаться.
Содержание:
- Что такое понятие?
- Виды понятий
- Отношения между понятиями
- Операции над понятиями
- Упражнения
- Проверочный тест
Что такое понятие?
Что такое понятие? Вроде бы интуитивно ясно. Возможно, многие скажут: понятие – это то же, что и слово или термин. Однако такое определение неверно. Понятия выражаются словами и терминами, но не идентичны им. Напомним, в прошлом уроке мы говорили, что все слова нашего языка – это знаки, обладающие двумя характеристиками: значением и смыслом. Обычно мы пользуемся языком интуитивно, не задумываясь о значении и смысле.
Мы просто называем одни объекты яблоками, другие грушами, третьи апельсинами. Часто мы выбираем то или иное слово, руководствуясь контекстом, то есть границы его употребления размыты. Между тем, нередки ситуации, когда такое интуитивное употребление слов неприемлемо или приводит к неприятным последствиям.
Представьте, например, что вы всей семьей собираетесь на отдых заграницу. Вы подаёте вместе документы на визу, и для этого вам нужно, чтобы ваш супруг (или ваша супруга) взял на работе справку о зарплате. Вы говорите ему: «Не забудь взять необходимую бумагу». Вечером он приносит вам пачку прекрасной бумаги А4.
В данной ситуации каждый из вас понял слово «бумага» по-своему, и это стало причиной обоюдного непонимания. Во многих сферах (законодательство, судопроизводство, должностные и технические инструкции, наука и т.п.) подобная двусмысленность должна быть исключена. Бороться с ней как раз и призваны понятия.
С точки зрения логики, понимать слово означает быть в состоянии указать, какие именно предметы им обозначаются, то есть уметь устанавливать относительно любого предмета, можно ли его назвать данным словом или нет. Каким образом этого достичь? Через образование понятия.
Понятие – это логическая мыслительная операция, которая по определённым признакам выделяет предметы из множества и объединяет их в один класс.
Таким образом, в образовании понятия участвуют три компонента: слово или словосочетание (знак), совокупность объектов, которые им обозначаются (значение), и некоторая идея или отличительный признак, связывающий данное слово с подпадающими под него объектами (смысл). Именно этот отличительный признак выступает сердцем понятия, потому что он связывает слово и объекты.
В качестве примера можно привести понятие квадрата. «Квадрат» – это термин, отличительный признак – «правильный четырёхугольник, у которого равны все углы и стороны», объекты – множество геометрических фигур, обладающих этим признаком. Что делает понятие квадрата? Из всего множества геометрических фигур оно выделяет какую-то группу фигур, потому что они обладают набором каких-то особых признаков.
Однако нужно учитывать, что для краткости люди чаще всего говорят просто о понятии квадрата или понятии человека, не уточняя, какой именно отличительный признак ложится в основу выделения этого понятия. Это часто приводит к разногласиям и так называемым спорам о словах. Поэтому прежде чем вступать в спор, полезно уточнить, какое именно понятие ваш собеседник вкладывает в то или иное слово.
Виды понятий
Каждое понятие обладает двумя характеристиками: содержанием и объёмом. Содержание понятия – это та совокупность отличительных признаков, на основании которой предметы выделяются из универсума и обобщаются в одну группу. Объём понятия – это совокупность всех предметов, которые обладают отличительными признаками.
Важно отметить, что объём понятия всегда задаётся относительно некоторого универсума рассмотрения, то есть множества объектов, которые в принципе могут обладать теми или иными отличительными признаками. Универсумом рассмотрения могут быть люди, живые существа, числа, химические соединения, бытовые приборы, науки, пищевые продукты и т.д. Так понятие «слоны» задаётся на универсуме живых существ, понятие «физика» – на универсуме наук, понятие «чётные числа» – на универсуме чисел, понятие «сыр» – на универсуме пищевых продуктов.
Содержание и объём понятия ложатся в основу разделения понятий на разные виды.
В зависимости от объёма понятия делятся на пустые и непустые. В объёме пустых понятий не содержится ни одного элемента. В объёме непустых понятий есть хотя бы один элемент. Если элемент всего один, то речь идёт о единичном понятии (автор «Войны и мира»), если их много – то об общих понятиях («французские короли»). Если объём понятия совпадает с универсумом рассмотрения, то говорят об универсальных понятиях («числа», «люди»)
Поговорим подробнее о пустых понятиях. Мы не всегда это замечаем, но пустые понятия используются людьми довольно часто. Это может происходить неосознанно, но иногда с их помощью нас стараются ввести в заблуждение. С одним примером пустого понятия мы уже сталкивались в прошлом уроке: «нынешний король Франции». Во всём универсуме людей нет ни одного человека, который обладал бы отличительным признаком «быть нынешним королём Франции». Нужно отметить, что в данном случае понятие оказалось пустым в силу исторического стечения обстоятельств.
Пойди история по-другому, это понятие могло бы быть непустым. Другой пример пустого понятия – «вечный двигатель». Здесь пустота обусловлена не историческими причинами, а законами природы. Что касается научных понятий, то относительно многих из них неизвестно, пустые они или нет. Хорошей иллюстрацией этому служит понятие «бозон Хиггса», непустота которого подтвердилась лишь недавно с открытием новой частицы, удовлетворяющей отличительным признакам этого понятия. Понятие может быть пустым и в силу законов логики. Это так называемые самопротиворечивые понятия, к примеру, «круглый квадрат».
Конкретными считаются понятия, элементами объёма которых являются индивиды или совокупности индивидов. Важно отметить, что под индивидами здесь понимаются не люди, а индивидуальные объекты, причём даже если эти объекты являются абстрактными сущностями. Поэтому примером конкретного понятия может быть «Солнечная система», «натуральные числа». К числу абстрактных понятий относят понятия, элементами объёма которых являются свойства, предметно-функциональные характеристики, отношения, например: «красота», «твёрдость».
По типу содержания понятия делятся на положительные и отрицательные, относительные и безотносительные. Отрицательные понятия содержат знак логического отрицания, положительные понятия, соответственно, не содержат его. Все примеры понятий, которые мы приводили, были положительными. Пример отрицательного понятия: «нечётные числа». Относительные понятия в качестве отличительного признака подпадающих под него объектов берут так называемые реляционные свойства, то есть свойства, образованные от некоторого отношения.
Примером относительного понятия будет человек как «существо, способное производить орудия труда». Среди относительных понятий можно выделить пары взаимосвязанных понятий, предполагающих друг друга: «учитель» и «ученик», «продавец» и «покупатель». Безотносительными называются понятия о предметах, отличительным признаком которых не является реляционное свойство, например: «цитрусовые фрукты».
Вся эта довольно сложная типология понятий нужна для того, чтобы мы могли с лёгкостью производить над понятиями операции и определять в каких отношениях друг к другу они находятся.
Отношения между понятиями
Понятия не изолированы друг от друга, наоборот, они находятся во множестве связей с другими понятиями. Умение выявлять эти связи очень важно, так как оно позволяет выявить, когда наш собеседник или автор текста ошибается в употреблении понятий или даже осознанно ими манипулирует. Примерами такой манипуляции могут послужить использование понятий, объёмы которых не равны, как взаимозаменяемых, незаметный переход к понятию с меньшим объёмом для облегчения доказательства своей позиции и т.д.
Прежде чем выяснять, в каком отношении находятся два понятия, нужно определить, сравнимы ли они вообще или нет.
Логики делят отношения между понятиями на фундаментальные и производные. Фундаментальные отношения первичны, с помощью их различных комбинаций можно задать все остальные отношения. Всего выделяют три фундаментальных отношения: совместимость, включение и исчерпывание.
Понятия совместимы, если пересечение их объёмов непусто. Соответственно, если пересечение их объёмов пусто, то понятия несовместимы.
Понятие А включается в понятие В, если каждый элемент объёма А также является элементом объёма В.
Понятия находятся в отношении исчерпывания, если и только если каждый предмет из универсума рассмотрения является элементом объема либо первого, либо второго понятия.
В результате комбинирования этих фундаментальных отношений можно задать пятнадцать производных отношений между понятиями. Мы расскажем только о тех из них, которые оперируют с непустыми и неуниверсальными понятиями. Их всего шесть.
Равнообъёмность – это отношение, при котором объёмы двух понятий полностью совпадают.
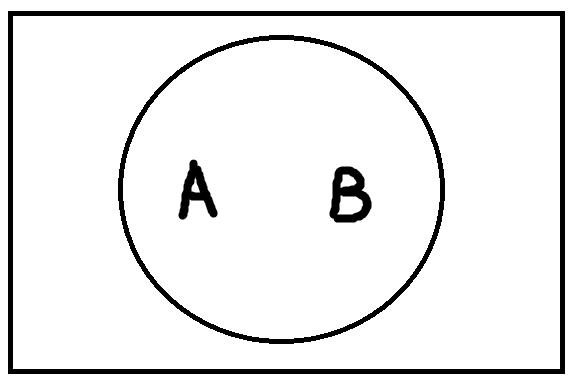
При равнообъёмности понятия А и В живут в одном кружочке. Примером может служить пара понятий: «треугольник с равными сторонами» и «треугольник с равными углами». Оба этих понятия обозначают одну и ту же совокупность объектов.
Подчинение возникает тогда, когда объём одного понятия полностью входит в объём другого понятия.
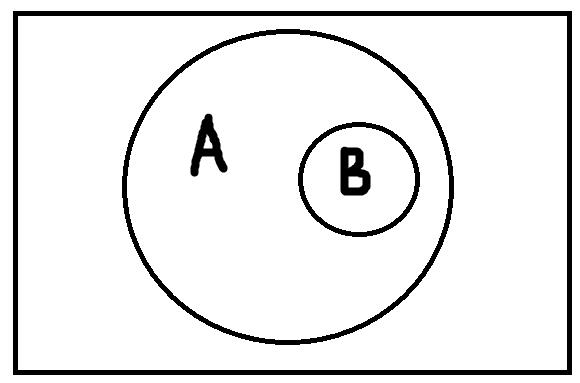
Кружочек В полностью располагается в кружочке А, и при этом кружочек А больше чем В по объёму, то есть в А входят объекты, которые не входят в В. Иллюстрация подчинения – отношения между понятиями «цитрусовые фрукты» (А) и «апельсины» (В).
Пересечение – это отношение, при котором объёмы понятий пересекаются, но полностью не совпадают.
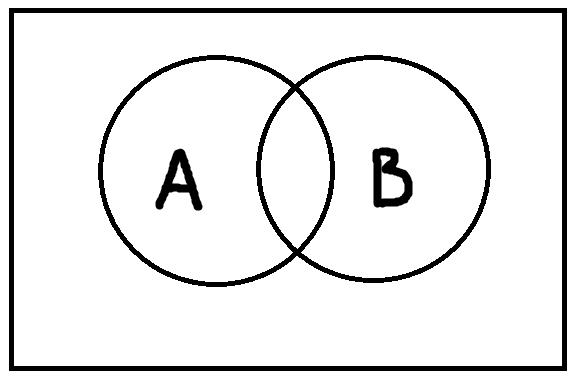
Пример пересечения – отношение между понятиями «женщины» и «руководители». Существуют люди, которые обладают и первой, и второй характеристикой.
Дополнительность – это такое отношение, когда два понятия пересекаются и при этом исчерпывают собой весь универсум рассмотрения.

Я специально изобразила понятия А и В разными цветами, чтобы было видно, что кружок в центре – это не отдельное понятие, а результат их пересечения. Отношение дополнительности существует, например, между понятиями «температура выше 0°С» и «температура ниже 30°С». Объёмы этих понятий пересекаются, и при этом объём их сложения равен объёму универсума рассмотрения.
Противоречие – это отношение, при котором объёмы понятий не пересекаются и исчерпывают весь универсум.
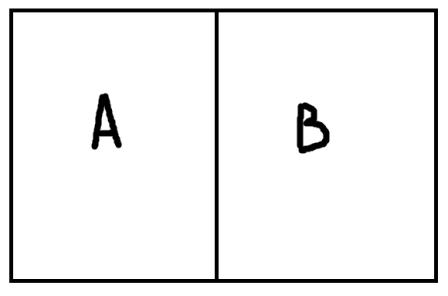
Если, к примеру, универсум рассмотрения – это люди, то А может быть понятием «работающие», а В – «безработные». Каждый человек может быть либо работающим, либо безработным, но не ими вместе и не чем-то третьим.
Соподчинение возникает, когда объёмы понятий не пересекаются, но при этом не исчерпывают собой весь универсум рассмотрения.
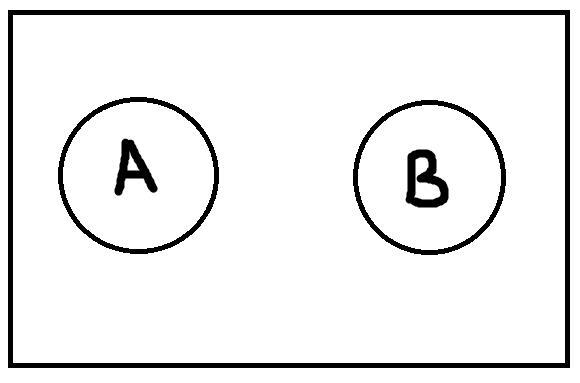
Сразу скажу, что я не знаю, чем руководствовались те, кто назвал это отношение соподчинением. На мой взгляд, речь скорее идёт о независимости друг от друга. Видимо, имеется в виду, что оба понятия находятся в отношении подчинения к какому-то третьему понятию – в данном случае всему универсуму рассмотрения. Предположим, что универсум рассмотрения – это животные. Тогда понятие А – «ящерицы», понятие В – «кошки». И ящерицы, и кошки – это животные. Объёмы этих понятий не пересекаются. При этом объём универсального понятия «животные» содержит множество не подпадающих под А и В элементов.
Закон обратного отношения между содержанием и объёмом понятия
В самом начале мы сказали, что понятие обладает двумя характеристиками: содержанием и объёмом. Соответственно, когда мы определяем отношение между понятиями, имеют значение не только их объёмные характеристики, но и содержательные. В частности, логики выяснили, что между объёмом и содержанием понятий существует так называемый закон обратного отношения. Суть этого закона состоит в следующем: если первое понятие ýже по объёму, чем второе понятие, то тогда первое понятие богаче второго по содержанию.
Если некий объект подпадает под понятие «ромашка», то мы автоматически знаем, что он также будет подпадать под понятие «цветы», а вот заключение в обратную сторону сделать нельзя. Если некий объект является элементом понятия «цветы», то это совсем не значит, что он также будет элементом понятия «ромашка». Он вполне может быть пионом, розой, лавандой и т.д.
Операции над понятиями
Главная цель операций над понятиями – образование нового понятия, со своим собственным объёмом и содержанием, из имеющихся других или более понятий. Основные операции, совершаемые над понятиями, называются булевыми операциями. Такое наименование они получили в честь английского математика и логика Дж. Буля, который разработал своеобразную логическую математику. Правда, операции, совершаемые над понятиями, похожи на те операции, которые мы научились выполнять с числами в начальной школе. К ним относятся: пересечение, объединение, вычитание, симметрическая разность, дополнение.
Пересечение понятий – это операция, в ходе которой берутся два или более понятий и как бы накладываются друг на друга. В результате в месте пересечения их объёмов образуется новое понятие, элементами которого будут те предметы, которые одновременно обладают отличительными признаками всех пересечённых понятий. Чтобы представить это наглядно, посмотрим на рисунки:
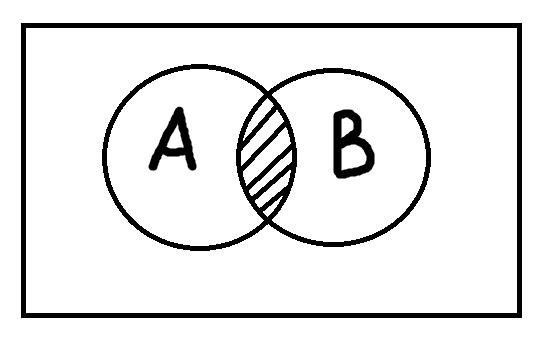
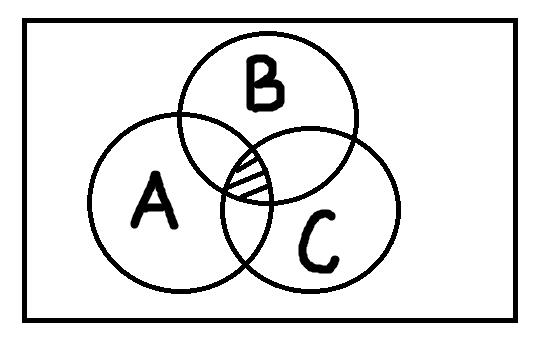
Результат пересечения – заштрихованная область. Например, если мы возьмём понятие «полицейские» и понятие «коррупционеры» и произведём над ними операцию пересечения, то в заштрихованной области окажутся только те люди, которые одновременно являются и полицейскими и коррупционерами. Так мы образовали новое понятие «полицейские-коррупционеры». Как видно, операция пересечения базируется на отношении пересечения. Это означает, что, если два понятия находятся в отношении пересечения, то мы легко можем образовать с их помощью новое понятие.
Объединение понятий подобно сложению: мы берём несколько понятий, соединяем их объёмы и тем самым образуем новое понятие, элементами которого будут те предметы, которые обладают хотя бы одним из отличительных признаков объединённых понятий.
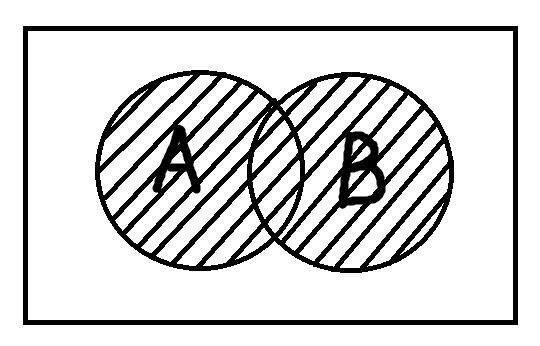
Для иллюстрации мы можем взять понятия «курильщики» и «люди, употребляющие алкоголь» и посредством объединения образовать понятие «люди, которые курят или употребляют алкоголь». В данном случае под понятие будут подпадать не только те люди, которые одновременно и курят, и пьют, но все те, кто обладает хотя бы одной из этих вредных привычек. Поэтому мы заштриховали оба кружочка.
Вычитание понятий опять же очень похоже на математическое вычитание. При вычитании берётся два или более понятий и из объёма одного отнимаются объёмы оставшихся. Таким образом, образуется новое понятие, элементами объёма которого будут предметы, обладающие отличительным признаком первого понятия, но не обладающие отличительными признаками тех понятий, которые из него вычитались.
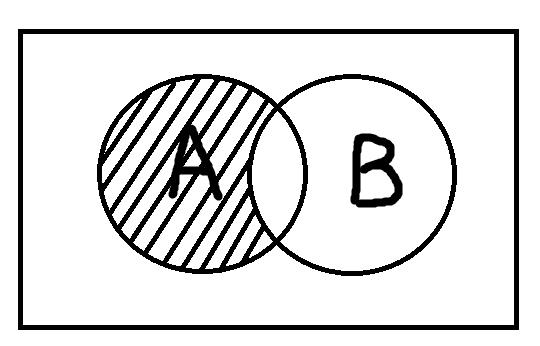
Предположим, что понятие А – это «люди, страдающие диабетом», понятие В – «люди, страдающие избыточным весом». Если мы вычитаем понятие В из понятия А, то мы получаем новое понятие «люди, страдающие диабетом, но не имеющие избыточного веса». Оно показано заштрихованной областью.
Симметрическая разность – это операция, в некотором смысле обратная пересечению. Нужно точно также взять два или более понятий, наложить их друг на друга, но новое понятие, образованное в результате этого наложения, будет содержать только те элементы, которые обладают не более чем одним отличительным признаком изначальных понятий.
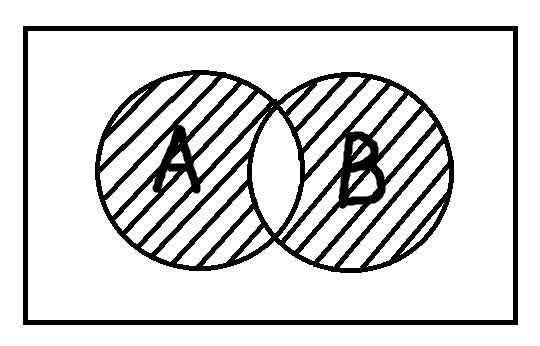
Заштрихованная область показывает это новое понятие. Предметы, подпадающие под это понятие должны обладать признаком А или В, но не ими вместе. Пусть А – это понятие «врач», В – «мужчина». Тогда получаем следующее понятие: «быть врачом, но не быть мужчиной, либо быть мужчиной, но не быть врачом».
Дополнение – это операция, в ходе которой берётся понятие, а затем его объём как бы вычитается из всего универсума рассмотрения. Так создаётся новое понятие, элементами которого будут только те предметы, которые не обладают отличительным признаком изначально взятого понятия.
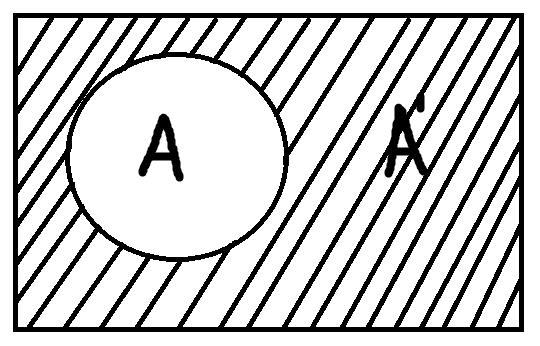
Новое понятие А’ – дополнение к понятию А. Если универсум нашего рассмотрения – это животные, понятие А – «млекопитающие», то А’ – «животные, не являющиеся млекопитающими». Операцию дополнения не нужно путать с отношением дополнительности.
Помимо булевых операций над понятиями можно проводить ещё целый ряд операций: ограничение, обобщение, деление.
Ограничение – это операция, представляющая собой как бы сужение понятия. Ограничить понятие А означает перейти к понятию В, такому что его объём будет строго включаться в объём понятия А. Причём этот переход от А к В представляет собой переход от родового понятия к видовому.
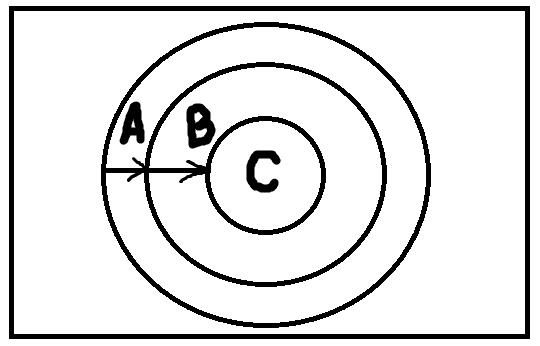
Как видно из картинки, в результате ограничения кружочек, представляющий объём понятия, становится меньше. Мы ограничиваем понятие А до понятия В, а затем – понятие В до понятия С. Можно предположить, что понятие А – это «рыбы». Мы можем ограничить его до понятия В – «акулы». Объём понятия А шире, так как рыбы бывают разные, они включают много видов – не только акул. При этом объём понятия В полностью включается в объём понятия А, потому что все акулы – это рыбы. Понятие «акулы» можно ограничить до понятия С – «белые акулы». Опять же понятие «белые акулы» полностью входит в понятие «акулы», но меньше его по объёму. Пределом ограничения понятия выступает единичное понятие. На нашем рисунке оно представляло бы точку в центре, которую уже нельзя сузить.
Операция ограничения понятий нередко сопровождается ошибками. Чаще всего они связаны с тем, что ограничение понятий путают с членением предметов, то есть понятие ограничивают не на основании родовидовых признаков, а на основании тех частей, на которые разделяются элементы их объёмов. Например, возьмём понятие «автомобили». По родовидовым признакам мы можем ограничить его до понятий «автомобили с ручной коробкой передач» или «электромобили». И это правильное ограничение.
Однако автомобиль состоит из множества компонентов: фары, колёса, руль, дворники, двигатель и т.д. Поэтому можно встретить такой вариант: понятие А – «автомобили» ограничивают до понятия В – «колёса». Хотя колёса – это часть автомобиля, такое ограничение неверно. Существует лёгкий способ избежать этой ошибки. При правильном ограничении понятия А до понятия В, должно быть верным высказывание «Все В есть А»: «Все акулы – это рыбы», «Все электромобили – это автомобили». Если мы применяем эту формулу к автомобилям и колёсами, получается: «Все колёса – это автомобили». Высказывание неверно, значит, операция ограничения была проведена неправильно.
Обобщение – это операция, обратная ограничению. На этот раз мы не сужаем, а расширяем понятие. Обобщить понятие В означает перейти к понятию А, так что объём понятия В будет строго включаться в объём понятия А. Здесь совершается переход от видового понятия к родовому.
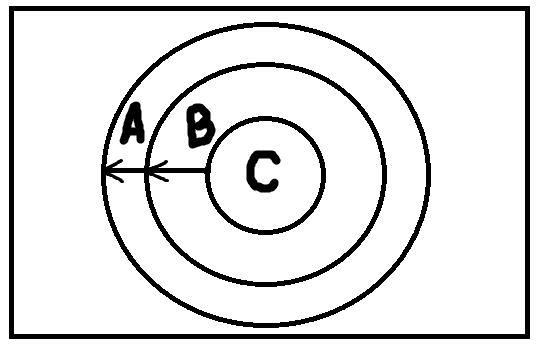
Понятие С, представленное самым маленьким кружочком, мы обобщаем до понятия В, которое в свою очередь мы можем ещё обобщить до понятия А, причём С полностью включается в В, и В полностью включается в А. Пусть С – это понятие «золото», тогда мы можем обобщить его до понятия В – «металлы», а понятие В – до понятия А – «химические элементы». Предел обобщения – это универсальное понятие, то есть понятие, объём которого совпадает с универсумом рассмотрения. В нашем примере понятие «химические элементы» как раз может быть рассмотрено как универсальное.
Деление – это операция, состоящая в том, что берётся понятие, выделяется какая-то характеристика и на основе варьирования этой характеристики исходное понятие делится на несколько частей, в результате чего получается набор новых понятий. Исходное понятие называют делимым понятием. Те понятия, которые образуются после деления – членами деления. Характеристику, на основе которой осуществляется деление – основанием деления.
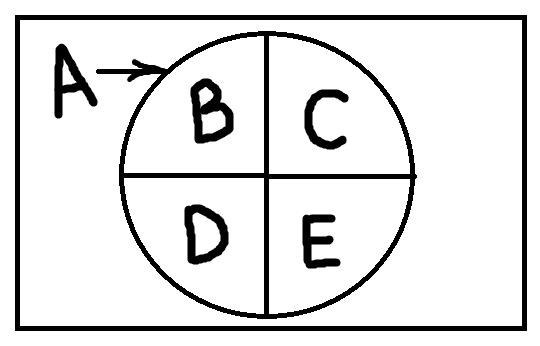
Весь кружочек – это объём понятия делимого понятия А. В, С, D и Е – члены деления, то есть понятия, образованные в результате деления понятия А. Для иллюстрации предположим, что понятие А – это «месяцы». Основание деления – это принадлежность к времени года. Тогда новообразовавшиеся понятия В, С, D и Е – это «зимние месяцы», «весенние месяцы», «летние месяцы» и «осенние месяцы». Очевидно, что в результате деления может получаться разное количество понятий: всё зависит от делимого понятия и основания деления.
Чтобы деление было правильным, необходимо соблюдать следующие условия:
| | Деление должно производиться только по одному основанию. Если использовать наш пример с понятием месяцы, то я не могу разделить его на следующие подпонятия: «зимние месяцы», «весенние месяцы», «летние месяцы», «осенние месяцы» и «мои любимые месяцы». В таком делении используются две характеристики: принадлежность к времени года и моё отношение к конкретному месяцу. Это называется путанным делением. Также если использовать больше, чем одно основание деления, можно совершить так называемый скачок в делении, состоящий в том, что одни члены деления являются видами А, а другие – его подвидами. Например, исходное понятие – «вино», основание деления – цвет. В результате правильного деления мы должны получить три новых понятия: «белое вино», «розовое вино» и «красное вино». Но если в делении совершён скачок, то можно прийти к такому результату: «белое вино», «розовое вино», «каберне», «шираз», «мерло», «пино нуар». В данном случае были совмещены два основания: цвет и сорт, и в члены деления одновременно попали виды вида (белое, розовое) и подвиды (каберне, шираз и т.д.). |
| | Члены деления В, С и т.д. должны представлять собой виды по отношению к родовому понятию А. Это то же условие, с которым мы сталкивались при ограничении и обобщении. Нельзя разделить понятие «автомобиль» на понятия «колёса», «двигатель», «руль» и т.п. Опять же нужно задаться вопросом, верно ли утверждение «Все В есть А», «Все С есть А» и так по всем членам деления. Если же вас всё-таки интересуют колёса и двигатель, то необходимо заменить делимое понятие на «части автомобиля», тогда деление станет правильным. |
| | Объёмы членов деления не пересекаются, то есть ни один из элементов не может одновременно попадать в В и С или в В и Е и т.д. |
| | Члены деления не могут быть пустыми понятиями. Предположим, что исходное понятие А – это «ныне правящие короли». Основание деления – принадлежность к странам. Так вот, среди членов деления не может быть понятий «ныне правящие французские короли» или «ныне правящие немецкие короли», так как это пустые понятия. |
| | Если над всеми членами деления B, C, D, E произвести операцию объединения, то мы должны получить объём делимого понятия A. |
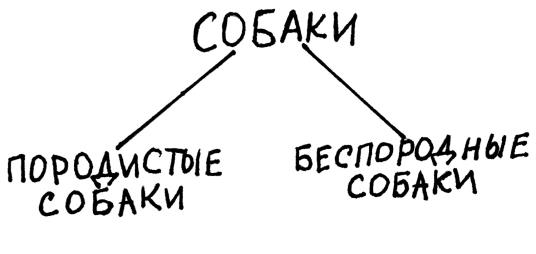
Существует два вида деления: дихотомическое деление и деление по видоизменению основания. Слово «дихотомический» дословно переводится с греческого как «деление надвое». При его осуществлении исходное понятие делится всего лишь на два новых понятия. Выбирается какое-либо основание деления, то есть признак, и в зависимости от наличия или отсутствия этого признака все элементы объёма разделяются на две части. Пусть делимым понятием будет понятие «люди», основанием деления – наличие высшего образования. В таком случае наше исходное понятие будет разделено на два: «люди, имеющее высшее образование» и «люди, не имеющие высшего образования». Другой пример: возьмём понятие «собаки», основание деления – породистость. В результате дихотомического деления получаем понятия: «породистые собаки», «беспородные собаки».
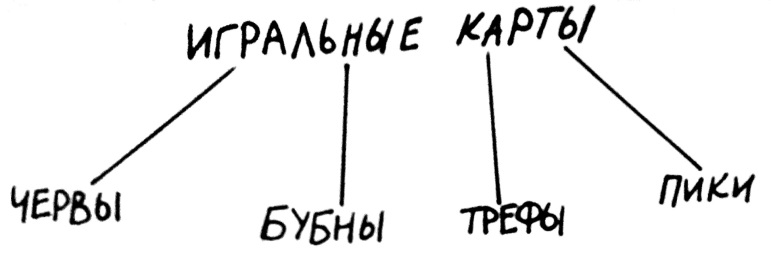
Второй вид деления – деление по видоизменению основания. В его результате мы можем получить более двух новых понятий. Здесь в качестве основания выбирается какая-либо предметно-функциональная характеристика элементов объёма исходного понятия. В нашем примере с месяцами такой характеристикой была принадлежность к времени года. Если наше делимое понятие – это «люди», то можно в качестве основания деления взять цвет глаз, цвет волос, национальность и т.п. Если делимое понятие – «стихотворения», то основанием деления может быть их жанровая принадлежность. Для иллюстрации возьмём понятие «игральные карты», а основанием деления сделаем масть:
Классификация. Операция деления лежит в основе составления классификаций и типологий. Классификация осуществляется посредством последовательного деления понятия на его виды, видов – на подвиды и т.д. Классификация, прежде всего, важна в научном познании. Она может выступать как результатом изучения какой-то предметной области (всеобщая классификация растений и животных Карла Линнея), так и двигателем исследований (периодическая таблица химических элементов Менделеева).
Кроме того, классификации очень важны в обучении.
Часто даже сами того не замечая, мы пользуемся классификациями и в повседневной жизни: ранжирование сотрудников в офисе, организация одежды в шкафу, распределение товаров по отделам в магазине – вот только несколько примеров.
Правильно выполненная классификация подобна перевёрнутому дереву (на мой взгляд, скорее, перевёрнутому кусту). Вершина классификации – исходное делимое понятие – называется корнем. Линии, расходящиеся от неё, подобны веткам. Они ведут к членам деления, от которых в свою очередь также расходятся ветки к новым понятиям. Каждое понятие в классификации называют таксоном. Таксоны группируются по ярусам. На первом ярусе находится корень классификации А. На втором ярусе – таксоны В1-Вn, образованные с помощью первой операции деления. На третьем ярусе – таксоны С1-Сn, образованные в результате второй операции деления и т.д. Каждый ярус может содержать любое количество таксонов.
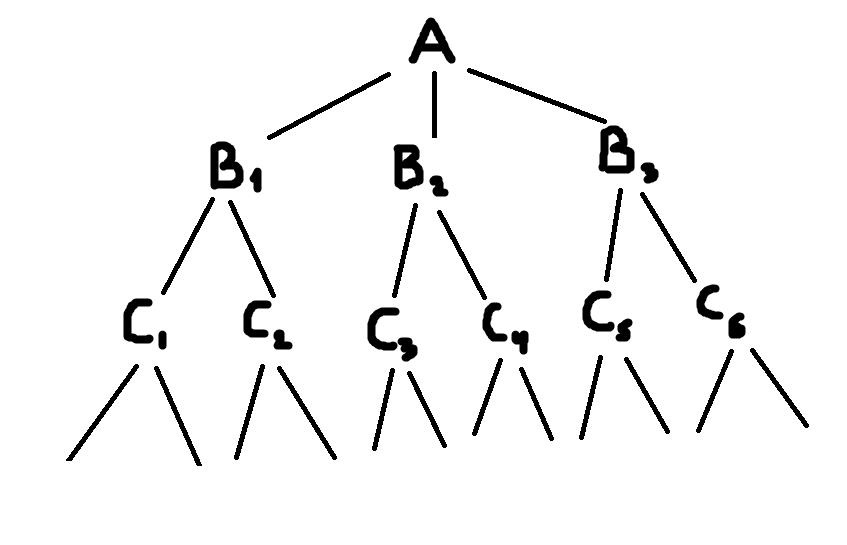
При построении классификаций используются оба вида деления: и дихотомическое, и по видоизменению основания. При этом они могут соседствовать даже в одной классификации. Дело в том, что внутри классификации каждая отдельная операция деления может производиться по своему собственному основанию. Приведём пример. Возьмём в качестве корня классификации понятие «писатели», основание деления – являлся ли писатель русским или нет. Соответственно, производим дихотомическое деление, в результате которого получаем на втором уровне два новых понятия: «русские писатели» и «зарубежные писатели».
Затем мы можем разделить понятие «русские писатели» по видоизменению основания. В качестве основания возьмём характеристику: «в каком веке жил писатель?» Получаем новые понятия: «русские писатели XIвека», «русские писатели XIIвека» и так вплоть до «русских писателей XXIвека». Что касается понятия «зарубежные писатели», то его тоже можно разделить по видоизменению основания, но в качестве основания взять национальность писателей. Таким образом, получим: «испанские писатели», «французские писатели», «немецкие писатели» и т.д.
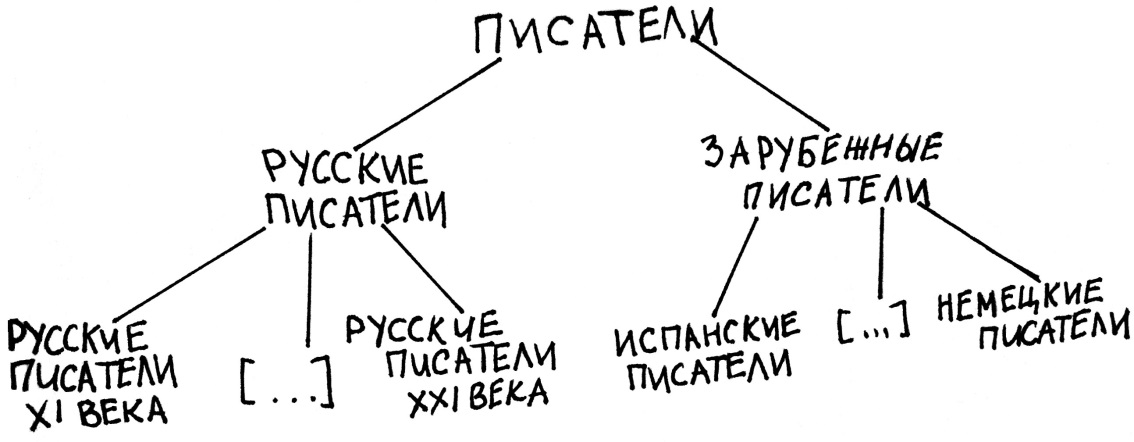
Знаком […] обозначены пропущенные члены деления. Дальше каждый таксон может быть разделён ещё по какому-то своему признаку. Главное в каждом отдельном делении соблюдать перечисленные выше правила.
Нужно отметить, что составление классификаций – не такая простая задача, как может показаться на первый взгляд. Не редки ситуации, когда сложно или невозможно определить, к какому именно таксону нужно относить тот или иной предмет. В нашем примере с писателями, в частности, возможны случаи, когда писатель родился и начал творить в одном веке, а умер уже в другом, как Чехов. Куда его нужно относить – в писатели XIXвека или XXвека? Иногда встречаются объекты, которые в принципе никуда не укладываются. Тогда для них создают отдельный таксон или помещают их в так называемый «отстойник». Он может обозначаться словами «всё прочее», и объекты, находящиеся в нём, не связаны ничем иным, кроме того, что их не удаётся никуда определить.
Упражнения
Китайская энциклопедия
Борхес в одном из своих произведений приводит отрывок из таинственной китайской энциклопедии. Это «божественное хранилище благотворных знаний» говорит, что «животные подразделяются на: а) принадлежащих Императору, б) бальзамированных, в) прирученных, г) молочных поросят, д) сирен, е) сказочных, ж) бродячих собак, з) включенных в настоящую классификацию, и) буйствующих, как в безумии, к) неисчислимых, л) нарисованных очень тонкой кисточкой из верблюжьей шерсти, м) и прочих, п) только что разбивших кувшин, о) издалека кажущихся мухами» (Борхес Х.Л. Аналитический язык Джона Уилкинса // Соч. в 3 т. Т. 2. Рига: Полярис, 1997, с. 85).
Попробуйте представить эту классификацию животных в виде дерева. Считаете ли вы, что она выполнена правильно? Если да, то докажите, что ни одно из правил деления в ней не нарушено. Если нет, то объясните, какие именно правила нарушены. Каким образом эту классификацию можно было бы исправить?
Мясо не еда
Кот. Прости, пожалуйста, за нескромность. Я тебя давно вот о чем хотел спросить…
Осел. Ну?
Кот. Как можешь ты есть колючки?
Осел. А что?
Кот. В траве попадаются, правда, съедобные стебельки. А колючки… сухие такие!
Осел. Ничего. Люблю острое.
Кот. А мясо?
Осел. Что – мясо?
Кот. Не пробовал есть?
Осел. Мясо – это не еда. Мясо – это поклажа. Его в тележку кладут, дурачок. (Е. Шварц, «Дракон»)
Определите отношения между понятиями «еда», «острые предметы», «острая еда», «колючки», «мясо» и «поклажа». Изобразите эти отношения с помощью графических схем. Помните, что понятия могут быть сравнимы, только если они принадлежат к одному универсуму рассмотрения.
Разговор мужа с женой
Муж: Милая, ты не права.
Жена: Ах, я не права. Значит, я лгу. Я лгу, значит, я плохой человек, то есть нелюдь. Ты хочешь сказать, что я животное? Мама, он меня скотиной назвал!
Определите, правильно ли был выполнен переход между понятиями «человек, который не прав», «лжец», «плохой человек», «нелюдь», «животное», «скотина». Обоснуйте свою позицию. Какие операции над понятиями использовались при этом переходе? В каких отношениях находятся эти понятия? Изобразите их с помощью графических схем.
Проверьте свои знания
Если вы хотите проверить свои знания по теме данного урока, можете пройти небольшой тест, состоящий из нескольких вопросов. В каждом вопросе правильным может быть только один вариант. После выбора вами одного из вариантов система автоматически переходит к следующему вопросу. На получаемые вами баллы влияет правильность ваших ответов и затраченное на прохождение время. Обратите внимание, что вопросы каждый раз разные, а варианты перемешиваются.
Следующий урок посвящен определению.

 Ксения Галанина
Ксения Галанина