Урок 5. Логические законы и противоречия

В прошлом уроке были рассмотрены условия истинности для категорических атрибутивных высказываний в силлогистике. Мы показали, что разные типы высказываний при одних условиях истинны, а при других – ложны. При этом нам ни разу не встречались высказывания, которые были бы всегда истинны или всегда ложны. Между тем, такие высказывания бывают. Первые называются логическими законами, а вторые – логическими противоречиями. О них мы и поговорим в этом уроке.

Во введении к курсу было сказано, что логика – это нормативная наука о формах и приёмах рациональной познавательной деятельности. Как и любая другая наука, логика также формулирует свои законы. Однако в отличие от других наук, законы эти являются нормативными, то есть они не описывают процесс человеческого мышления, а предписывают, как человек должен мыслить, если он хочет, чтобы его рассуждение было корректным. Таким образом, логические законы представляют собой некие общие принципы, которыми люди должны руководствоваться в процессе рассуждения.

Если попытаться дать более строгое определение, то:

Логический закон – это определённая логическая форма, благодаря которой высказывание в целом принимает значение «истина», независимо от конкретного содержания его частей.

По этой причине логические законы также иногда называют логическими тавтологиями: о чём бы мы не говорили, высказывания, имеющие форму логических законов, всегда оказываются истинными. К тому же они кажутся «бесплодными», потому что мы не можем извлечь из них никакой реальной информации о мире.

Логические противоречия – полная противоположность логическим законам, то есть это такая логическая форма, при которой высказывание в целом всегда принимает значение «ложь», независимо от содержания его частей.

Содержание:

• Таблицы истинности
• Логические законы
• Закон тождества
• Закон противоречия
• Закон исключения третьего
• Проверочный тест

Таблицы истинности

Как же определить, что определённое высказывание всегда принимает значение «истина» или «ложь»? Логики придумали для этого очень удобный метод, который получил название «таблиц истинности». Как понятно из названия, они представляют собой таблицы, в которых в верхнюю строку записывается логическая форма высказываний, а в столбцы под каждым компонентом записываются их истинностные значения. Давайте построим таблицу истинности для высказывания «Идёт дождь».

Здесь всё довольно ясно: «Идёт дождь» – это простое высказывание, которое может принимать значение либо «истина», либо «ложь». Обычно для удобства логики сокращают значения до «и» и «л», а само высказывание записывают маленькой буквой латинского алфавита: p, q, r, s и т.д. Поэтому в классическом виде таблица истинности для одного простого высказывания будет выглядеть так:

Давайте теперь представим, что у нас есть два высказывания: «Идёт дождь» и «Светит солнце». Пока они никаким образом не связаны между собой. Однако поскольку их уже два, то у нас возможны уже не две, а четыре комбинации: оба высказывания истинны, оба высказывания ложны, истинно либо первое, либо второе высказывание. Таблица истинности для них будет включать уже четыре строки для значений.

Если у нас есть три высказывания («Идёт дождь», «Светит солнце», «Трава зеленеет»), то таблица будет включать уже восемь строк для значений, так как в таком случае возможны восемь комбинаций.

Чем больше разных высказываний вы хотите рассмотреть, тем больше комбинаций из значений возможно. Число этих комбинаций для n высказываний вычисляется по формуле 2ⁿ. Так для четырёх высказываний, число комбинаций – шестнадцать, для пяти – тридцать два и т.д.

Таблицы истинности строятся и в силлогистике, однако выглядят они немного иначе. В левый столбец обычно помещается диаграмма, изображающая то или иное отношение между терминами S и P, а справа помещаются различные типы высказываний и их истинностные значения.

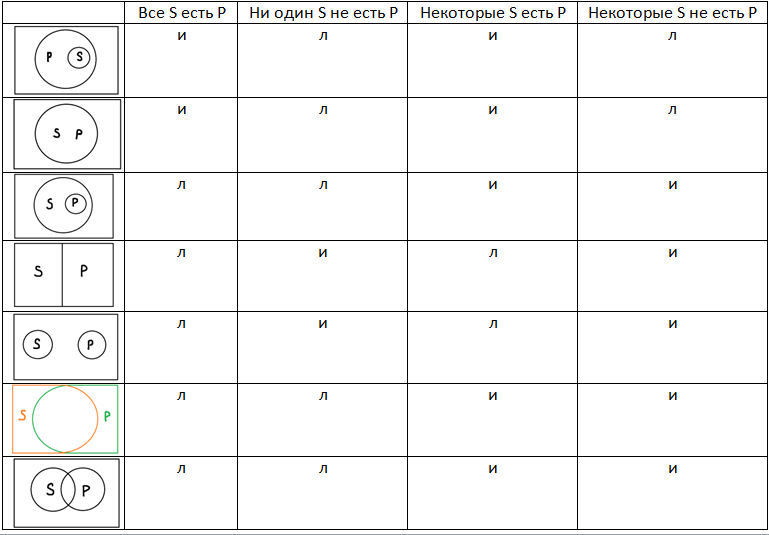
Это сводная таблица истинности для всех типов атрибутивных высказываний, которые мы обсуждали в прошлом уроке (единичные высказывания не включены отдельно, так как их условия истинности приравниваются к условиям истинности для общих высказываний).

Далее, понятно, что обычно в рассуждении высказывания каким-то образом связаны между собой с помощью пропозициональных связок. Мы зададим истинностные значения для основных связок, которые используются чаще всего в естественном языке.

Логическое отрицание используется, когда в высказывании отрицается наличие некоторой ситуации в мире, говорится об её отсутствии.

Например, «Дождь не идёт», «Комната была небольшой», «Неправда, что они друзья». В логике обычно передается через выражения «неверно, что p» или просто «не-p».

Как видно из таблицы, если высказывание истинно, то его отрицание будет принимать значение «ложь», если же высказывание само по себе ложно, то – «истина». Предположим, что вместо p мы имеем высказывание «Маргарет Тэтчер была первой и на настоящий момент единственной женщиной-премьер-министром Великобритании». Это истинное высказывание. Соответственно, если взять его отрицание: «Маргарет Тэтчер не была первой и на настоящий момент единственной женщиной-премьер-министром Великобритании», то оно будет ложным. Если же взять высказывание «Все болезни от нервов», которое является ложным, то его отрицание «Неверно, что все болезни от нервов» будет истинным.

Примеры конъюнкции можно увидеть в высказываниях «Пошёл дождь, и я спрятался под навес», «Витя хотел пойти в кино, а я хотел поиграть в футбол», «Белкин ждал директора целый час, но так и не дождался». Как видно, конъюнкция соединяет два или более простых высказываний в одно сложное.

Конъюнктивное высказывание может быть истинным, только если все его части истинны. Если хотя бы одно простое высказывание, входящее в её состав ложно, то тогда и конъюнкция в целом ложна. Пример истинной конъюнкции: «44-го президента США зовут Барак, а его жену – Мишель». Все следующие высказывания будут ложными: «44-го президента США зовут Барак, а его жену – Мэгги», «44-го президента США зовут Борат, а его жену – Мишель», «44-го президента США зовут Джон, а его жену – Элен».

Дизъюнкция утверждает, что хотя бы одна из двух или более ситуаций имеет место. В естественном языке она выражается словами «или» и «либо».

Примеры дизъюнктивных высказываний: «Маша была замужем за Анатолием или за Николаем», «Он работает над проектом ИК-25 либо ПФ-40». Хотя это не так очевидно, как в случае с конъюнкцией, дизъюнкция также объединяет в одно сложное высказывание два или более простых высказывания. Если мы выявляем логическую форму, то правильной была бы запись: «Маша была замужем за Анатолием, или Маша была замужем за Николаем».

Из таблицы понятно, что дизъюнкция ложна, только когда все простые высказывания, входящие в её состав ложны. К примеру, ложным будет высказывание «Уганда находится в Центральной Америке или Западной Европе». Когда хотя бы одна из частей дизъюнкции истина, она в целом также будет истинной. Например, истинным является высказывание «Нот всего семь или шесть».

При этом важно отметить, что выражение «хотя бы одна» подразумевает, что и обе части могут быть истинными. Иллюстрацией может служить следующее высказывание: «Велосипеды бывают двухколёсными или трёхколесными». Велосипеды бывают и такими, и другими, поэтому высказывание истинно. Однако нередки случаи, когда мы хотим указать, что лишь одна из альтернатив истинна, но никак не обе вместе.

Рассмотрим высказывание «Картина “Герника” принадлежит кисти Пикассо или Тициана». Здесь либо одно, либо другое. Они даже не могли написать её вместе, так как жили в разных веках. В таких ситуациях говорят о строгой дизъюнкции, которая будет истинна исключительно при истинности одного из её членов. Обычно она выражается словами «либо, либо».

«Если Люся – полная отличница, то и по математике у неё должна быть пятёрка». Смысл импликации состоит в том, что если первое простое высказывание верно, то и второе тоже будет верным.

Попробуем разобраться с этой таблицей. Проблема в том, что истинностные значения материальной импликации, в отличие от значений других пропозициональных связок, совсем не являются интуитивными. С первой строкой всё ясно: если первое высказывание верно, и второе высказывание верно, то импликация в целом тоже верна.

Пример: «Если птицы улетают на юг, то, значит, наступила осень». Со второй строкой тоже всё более или менее понятно: если первое высказывание истинно, а второе ложно, то отношения следования между ними нет. Вспомните отрывок из «Золотого ключика», в котором Мальвина пытается научить Буратино арифметике:

– Предположим у вас в кармане два яблока, и некто забрал у вас одно из них. Сколько у вас останется яблок?
– Два.
– Но почему?
– Ведь я не отдам Некту яблоко, пусть он и дерись!

Рассуждения Буратино можно представить в виде высказывания «Если некто забрал одно из имеющихся у меня двух яблок, у меня всё равно осталось два яблока». Если первая часть истинна, то вторая, безусловно, ложна, а потому и импликация в целом ложна. Способностей к арифметике у Буратино, действительно, не было.

С последними двумя строчками дело обстоит сложнее. Проблема в том, что для них сложно придумать пример на естественном языке. Когда логики формулировали значение материальной импликации, они пользовались математическим примером. Они взяли высказывание «Для всякого числа верно, что если оно кратно 4, то оно кратно и двум».

Если это высказывание верно для всякого числа, то оно должно быть верным и для любого конкретного числа: 5, 6, 8, 12 и т.д. Если подставить в высказывание 8, то получим: «если 8 кратно 4, то оно кратно и 2». Здесь и первая, и вторая части истинны. Мы получили первую строку. Если подставить число 6, «если 6 кратно 4, то оно кратно и 2», то мы получаем третью строку (первая часть ложна, а вторая истинна). Если подставить 5, «если 5 кратно 4, то 5 кратно и двум», то выходит последняя строка (обе части ложны).

Однако мы всё же можем подобрать примеры для всех этих ситуации, поэтому импликация истинна. Но вот для второй строки пример подобрать нельзя: нет такого числа, которое было бы кратно 4, но некратно 2. Поэтому вторая строка ложна.

Итак, мы разобрали истинностные значения основных связок, теперь мы можем посмотреть, какие их комбинации приведут к тому, что высказывание подобной формы будет всегда истинным, независимо от его содержания, другими словами – будет логическим законом.

Логические законы

Сразу стоит оговориться, что логических законов довольно много. Кроме того, обычно они формулируются в рамках конкретной логической системы: логики высказываний, логики предикатов, силлогистики, модальной логики и т.д. То, что является законом в одной системе, совсем необязательно будет законом в другой системе. Однако существует несколько основных законов, которые будут верны в любой логической системе. О них мы и расскажем.

Закон тождества

Закон тождества обычно формулируется в виде формулы «А есть А» или «Если А, то А».

Проверим этот закон с помощью таблицы истинности. Во-первых, у нас всего одно выражение – А, поэтому таблица будет включать только две комбинации: А истинно и А ложно. Во-вторых, связка «Если …, то …» выступает как знак материальной импликации. Таким образом, мы должны взять первую и последнюю строку из таблицы для материальной импликации.

Закон тождества также может быть сформулирован и в силлогистике для высказываний «Все А есть А» и «Некоторые А есть А»:

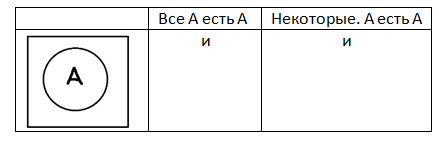
Какой бы термин мы не подставили на место А, высказывания, имеющие эти формы, всегда будут истинными: «Все кошки – это кошки», «Все туфли – это туфли», «Некоторые автомобили – это автомобили», «Некоторые дома – это дома» и т.п.

Если я утверждаю, что какое-то высказывание истинно, например, что высказывание «Красота спасёт мир» истинно, я не могу следующим шагом утверждать, что оно ложно. И наоборот, если я утверждаю, что какое-то высказывание ложно, оно не может вдруг ни с того ни с сего превратиться в истинное. Рассуждение должно быть последовательным.

Чаще всего закон тождества нарушается при так называемой подмене понятий: в ходе рассуждения используется один и тот же термин, но значения в него вкладываются каждый раз разные. К примеру, возьмём следующее рассуждение: «Знание – сила. Сила – это векторная физическая величина, мера интенсивности воздействия на данное тело других тел и полей. Следовательно, знание – это векторная физическая величина, мера интенсивности воздействия на данное тело других тел и полей». Такое рассуждение не может быть верным, так как здесь нарушен принцип тождества: термин «сила» употребляется в первом и втором предложении в разных значениях.

Закон противоречия

Закон противоречия гласит: неверно, что А и не-А.

Построим таблицу истинности.

В первом столбце даны значения А («истина» и «ложь»). Соответственно, мы просто копируем эти значения в третий столбец. Значения для не-А в пятом столбце будут прямо обратными для значений А, поэтому получаем «ложь», «истина». В четвёртом столбце располагается конъюнкция между А и не-А. Она не может быть истинной ни в одном из случаев. Поэтому её значение всегда «ложь». Наконец, второй столбец представляет значение выражения полностью – это отрицание конъюнкции между А и не-А. Поскольку конъюнкция ложна, то её отрицание будет истинным. В итоге, мы видим, что выражение в целом всегда истинно.

Если же мы возьмём выражение типа «А и не-А», то оно как раз будет представлять собой противоречие. Из таблицы мы видим, что такое выражение всегда будет принимать значение «ложь».

Согласно закону противоречия (иногда его называют законом непротиворечия) невозможно,  чтобы одновременно оказались истинными высказывание и его прямое отрицание: неверно, что снег идёт и в то же время не идёт, неверно, что Катя любит ананасы и не любит ананасы. Важно сделать следующее замечание: противоречия возникает только тогда, когда утверждение и отрицание делаются об одном и том же объекте, в одно и то же время, в одном и тот же отношении.

Например, высказывания «Снег идёт на Северном полюсе, но снег не идёт в Зимбабве», «Толя ходил в кино вчера, а сегодня не ходил», «Катя любит ананасы, а Петя не любит ананасы», «Вася любит кататься на коньках и не любит кататься на лыжах» не являются противоречиями. Все они говорят либо о разных предметах, либо о разных временных отрезках, либо о разных аспектах одного предмета. Поэтому не всё, что выглядит как противоречие, действительно является таковым. Такие кажущиеся противоречия называют мнимыми. Пример мнимого противоречия можно найти в дзенской притче «Бокудзю и ручей»:
 

Один дзэнский монах, Бокудзю, говорил: «Иди и пересеки ручей, но не позволяй воде прикоснуться к тебе». 
А через ручей около его монастыря не было никакого моста. Многие пытались сделать это, но когда они пересекали ручей, то, конечно же, вода прикасалась к ним. Поэтому однажды один монах пришел к нему и сказал: 
— Вы задали нам неразрешимую задачу. Мы пытаемся пересечь этот ручей; через него нет никакого моста. Если бы был мост, то мы, конечно же, пересекли бы ручей, и вода не прикоснулась бы к нам. Но мы вынуждены идти через поток, и вода прикасается к нам. 
И Бокудзю сказал: 
— Я пойду и пересеку его, а вы наблюдайте. 
И Бокудзю пересёк ручей. Вода, конечно, прикоснулась к его ногам, и они сказали: 
— Смотрите, вода прикоснулась к вам! 
Бокудзю сказал: 
— Насколько я знаю, она не прикоснулась ко мне. Я был просто свидетелем. Вода прикоснулась к моим ногам, но не ко мне. Я был просто свидетельствующим.

Между тем, чтобы пересечь ручей без моста и не позволить воде прикоснуться к себе, нет противоречия, потому что в данном случае человеческое я рассматривает в разных отношениях: как тело, и как дух. Тело проходит через ручей и намокает, но дух остаётся безмятежным и не затронутым водой.

Как и закон тождества, закон противоречия требует от нас быть последовательными в рассуждениях. Либо мы принимаем, что высказывание истинно, либо мы принимаем, что оно ложно, но не то и другое вместе. Смешение истины и лжи приводит к тому, что всё рассуждение обесценивается, так как мы уже не можем быть уверены в сделанном выводе.

Противоречия опасны потому, что с точки зрения логики из них можно вывести всё что угодно, то есть высказывание формы «Если А и не-А, то В» всегда будет истинным. Вы можете сами проверить это с помощью таблицы истинности. «Если дождь идёт, и дождь не идёт, то Чехов – автор “Войны и мира”». Если допускать противоречия, подобное «рассуждение» оказывается возможным. Поэтому логика ставит запрет на противоречия.

Обычно появление противоречия – это знак того, что в рассуждение где-то закралась ошибка. Исправление этой ошибки, снимет и противоречие. Ошибка может скрываться в сделанных умозаключениях, но может содержаться и в изначально избранных посылках. По этой причине приведение к противоречию играет ключевую роль в так называемых доказательствах от противного. Наверное, все помнят их со школьных уроков геометрии.

Доказательство от противного строится на том, что нужно обосновать какой-то тезис, но прямое его доказательство найти не получается. Тогда берётся его отрицание, и в определённый момент рассуждения мы наталкиваемся на противоречие, а это знак того, что отрицание тезиса было неверным. Так что противоречие может играть и позитивную роль в рассуждении.

В заключение, добавим, что в советской философии, превозносившей Маркса и Гегеля, появилось целое направление под названием «диалектическая логика», которая якобы допускала наличие противоречий и даже оценивала их положительно. Такая точка зрения строилась на том, что противоречия – это источник движения и развития, а потому это хорошо, если мы сталкиваемся с ними. Ещё и сегодня можно встретить людей, которые придерживаются подобного мнения.

Однако нужно понимать, что речь здесь не идёт о противоречии в логическом смысле (как форме высказывания, которое при любой интерпретации принимает значение «ложь»). Скорее, под противоречием тут следует мыслить несовместимость, плохую сочетаемость ситуаций, феноменов, характеров и т.д. Так во Франции конца XVIII века желание буржуазии участвовать в политической жизни страны плохо сочеталось с формой правления абсолютной монархии, что в итоге привело к буржуазной революции. Можно сказать, что между ними возникло противоречие, но это не имеет никакого отношения к логике.

Закон исключённого третьего

Закон исключённого третьего имеет следующую форму: А или неверно, что А.

Построим таблицу истинности:

Если А принимает значение «истина» и «ложь», то «неверно, что А» соответственно будет принимать значения «ложь» и «истина». Их дизъюнкция всегда будет истинной.

Закон исключённого третьего очень похож на закон противоречия, потому что он точно также утверждает, что высказывание и его отрицание не могут быть одновременно истинными. Истинно либо одно, либо другое, и третьего не дано. Истинно или высказывание «Глинка был композитором», или его отрицание «Глинка не был композитором», но они не могут быть истинными одновременно. Опять же здесь также стоит следить за тем, чтобы высказывания относились к одному и тому же предмету, говорили о нём в одном и том же отношении и в одно и то же время.

Нужно отметить, что законом исключённого третьего часто пользуются в качестве уловки, пытаясь представить какую-либо сложную ситуацию в виде простой оппозиции. К примеру: «Ты с нами или ты против нас», «Женщины бывают либо умными, либо красивыми», «Они либо патриоты, либо предатели». Особенно часто этим приёмом любят пользоваться политики, пытаясь представить, будто их оппоненты защищают какую-то радикальную позицию, которой те на самом деле не придерживаются. Отчасти эта склонность сводить всё многообразие фактов и позиций к двум противоположностям обусловлена чисто психологическими механизмами работы человеческого мышления.

Всё дело в том, что наше мышление работает по так называемому принципу когнитивной экономии: вместо того, чтобы тратить время и энергию на анализ всей сложности ситуации, мы предпочитаем представить её в виде грубой полярной схемы. Поэтому если ваш собеседник или демагог из телевизора говорит вам, что «третьего не дано», подумайте, так ли это: не заключается ли между двумя членами оппозиции целый спектр разнообразных возможностей.

Кроме того, с законом исключённого третьего нужно быть аккуратными ещё и потому, что значения высказываний во многих случаях определяются относительно конкретного контекста. Помните Ивана и его детей из прошлого урока? Вполне можно было бы сказать в соответствии с законом исключённого третьего: «Дети Ивана либо лысы, либо нет, третьего не дано». Но ни одна из этих альтернатив не может нас удовлетворить, так как у Ивана нет детей. Таким образом, прежде чем применять закон исключённого третьего, сверьтесь с контекстом высказывания.

Законы тождества, противоречия и исключённого третьего фундаментальны и выполняются в любых логических системах. Без соблюдения этих законов невозможно делать правильные умозаключения. Иногда к ним присоединяют ещё так называемый закон достаточного основания. Этот закон гласит, что любое утверждение должно быть корректно обосновано.

Хотя это очень важный принцип, на котором должны базироваться любые рассуждения, законом в собственно логическом смысле он не является, так как не представим в виде логической формы, которая при любой трактовке принимала бы значение «истина». Скорее, это общее требование, вытекающее из самой идеи логичного рассуждения, целью которого как раз и является обоснование тезиса путём правильных умозаключений. О том, как правильно делать умозаключения, мы начнём рассказывать в следующем уроке. 

Проверьте свои знания

Если вы хотите проверить свои знания по теме данного урока, можете пройти небольшой тест, состоящий из нескольких вопросов. В каждом вопросе правильным может быть только один вариант. После выбора вами одного из вариантов система автоматически переходит к следующему вопросу. На получаемые вами баллы влияет правильность ваших ответов и затраченное на прохождение время. Обратите внимание, что вопросы каждый раз разные, а варианты перемешиваются.

Далее поговорим об умозаключениях.

Ксения Галанина