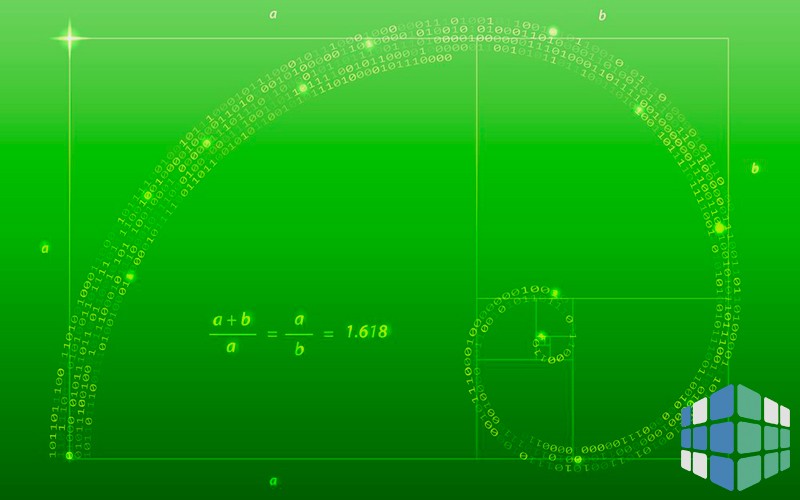
Золотым сечением называют число, полученное путем деления линии на две части таким образом, что более длинная часть (а), разделенная на меньшую часть (b), равна полной длине линии (а+b), разделенной на более длинную часть (а). Такое отношение часто символизируют с помощью литеры Ф (читается как «фи») – 21-й буквы греческого алфавита. В форме уравнения это выглядит так:
a / b = (a + b) / a = 1.6180339887498948420…
Как и в случае с π (пи, отношение длины окружности к ее диаметру), число Ф является бесконечным. Обычно его округляют до значения 1,618.
История открытия золотой середины
Это число было найдено и открыто много раз, поэтому у него так много разных названий - золотая середина, золотое сечение, божественная пропорция и т.д. Исторически его можно увидеть в архитектуре многих древних творений, таких как Великие Пирамиды и Парфенон. В пирамиде Гизы длина каждой стороны основания составляет 230,5 метров при высоте 146,6 метров. Отношение основания к высоте составляет примерно 1,5717, что близко к золотой пропорции.
Фидий (500 г. до н.э. - 432 г. до н.э.) был греческим скульптором и математиком, который, как считается, применил Ф, создавая скульптуры для Парфенона. Платон (428 г. до н.э. - 347 г. до н.э.) считал, что золотое сечение является наиболее универсальным связующим звеном математических отношений. Позднее Евклид (365 г. до н.э. - 300 г. до н.э.) связал золотое сечение с построением пентаграммы.
Последовательность Фибоначчи и золотое сечение
Около 1200 года математик Леонардо Фибоначчи открыл уникальные свойства последовательности Фибоначчи. Эта последовательность непосредственно связана с золотым сечением, потому что если взять любые два последовательных числа Фибоначчи, их отношение будет очень близко к золотому сечению. По мере того как числа возрастают, соотношение приближается к значению 1,618. Например, соотношение 3 к 5 составляет 1,666. Но соотношение 13 к 21 составляет 1,625. Возрастая, соотношение 144 к 233 составляет 1,618. Все эти числа являются последовательными числами в последовательности Фибоначчи.
Такие соотношения из ряда Фибоначчи, близкие к значению золотого сечения, могут быть применены к пропорциям прямоугольника, называемого золотым прямоугольником. Он известен как одна из наиболее визуально совершенных из всех геометрических форм - следовательно, правило золотого сечения очень широко применяется во всех видах визуального искусства. Золотой прямоугольник также связан с золотой спиралью, которая создается путем создания смежных квадратов измерений Фибоначчи.
Пропорции золотого сечения в материальном мире
В 1509 году Лука Пачоли написал книгу, которая называет число Ф «Божественной пропорцией», что было наглядно показано Леонардо да Винчи. Позже да Винчи назвал эту пропорцию золотым сечением. Оно использовалось для достижения баланса и красоты во многих картинах и скульптурах эпохи Возрождения.
Да Винчи сам использовал золотое сечение, чтобы определить все пропорции в «Тайной вечере», включая размеры стола, пропорции стен и деталей интерьера. Золотое сечение также появляется в «Витрувианском Человеке» да Винчи и «Мона Лизе». Считается, что золотое сечение использовали и другие великие художники, включая Микеланджело, Рафаэля, Рембрандта, Сьюрата и Сальвадора Дали.
Термин «фи» был придуман американским математиком Марком Барром в 1900-х годах. Ф продолжал применяться в математике и физике, в том числе в плитках Пенроуза 1970-х годов, которые позволяли мозаичным поверхностям иметь пятикратную симметрию. В 1980-х годах Ф появился в квазикристаллах – недавно открывшейся форме материи.
Фи - более чем загадочный и неясный термин в математике и физике. Он появляется вокруг нас в нашей повседневной жизни, даже в наших эстетических взглядах. Исследования показали, что когда испытуемые видят случайные лица, они считают наиболее привлекательными те, которые имеют четкие параллели с золотым сечением. Лица, оцененные как наиболее привлекательные, показывают золотые соотношения между шириной лица и шириной глаз, носа и бровей. Испытуемые не были математиками или физиками, знакомыми с правилом золотого сечения (они были просто среднестатистическими людьми), и оно вызвало инстинктивную реакцию.
Золотое сечение также проявляется во всех видах природы и науки. Ниже приведены примеры самых неожиданных мест, в которых можно его встретить.
- Цветочные лепестки. Количество лепестков на некоторых цветах соответствует последовательности Фибоначчи. С точки зрения теории Дарвина считается, что каждый лепесток помещается таким образом, чтобы обеспечить максимально возможное воздействие солнечного света и других факторов.
- Семенные головки. Семена цветка часто начинают произрастать в центре семенной головки и мигрируют наружу, заполняя свободное пространство. Например, семечки подсолнухов следуют этой схеме.
- Сосновые шишки. Семенные коробочки сосновых шишек наполнены семенами, которые растут спирально вверх, в противоположных направлениях. Количество шагов, которые делают спирали, как правило, соответствует числам Фибоначчи.
- Ветви дерева. То, как ветки дерева формируются или расщепляются, является примером последовательности Фибоначчи. Корневые системы и водоросли также придерживаются такого способа формирования.
- Раковины. Многие раковины, в том числе раковины улитки и раковины наутилуса, являются прекрасными примерами золотой спирали.
- Спиральные галактики. Млечный путь имеет несколько спиральных рукавов, каждый из которых имеет логарифмическую спираль примерно 12 градусов. Форма спирали идентична золотой спирали, а золотой прямоугольник можно нарисовать над любой спиральной галактикой.
- Ураганы. Внутреннее строение ураганов часто следует правилу золотой спирали.
- Пальцы руки человека. Каждый участок пальца от кончика основания до запястья больше, чем предыдущий, примерно на соотношение Ф.
- Тела человека и животных. Расстояние от пупка человека до пола и от макушки головы до пупка – это золотое сечение. Но человек не единственный пример золотого сечения в животном мире. Дельфины, морские звезды, морские ежи, муравьи и пчелы также демонстрируют эту пропорцию.
- Молекулы ДНК. Молекула ДНК имеет размеры 34 ангстрем на 21 ангстрем на каждом полном цикле спирали в виде сдвоенной спирали. В рядах Фибоначчи 34 и 21 являются последовательными числами.
Таким образом, примеров, где встречаются пропорции и соотношения, следующие правилу золотого сечения, более чем достаточно. Кроме перечисленных примеров, число «Фи» часто встречается в математике, физике, астрономии, биологии и иных сферах деятельности человека. Можно смело утверждать, что название «Божественное сечение» по праву присвоено числу Ф – видимо им руководствовался создатель, наполняя эту Вселенную всем живым и неживым.