Представьте, что вам предложили сыграть в одну несложную и весьма зажигательную игру. По сути, та же «Орел и решка», зато какая! Ваш выигрыш растет в геометрической прогрессии каждый раз, когда выпадает решка, и так до тех пор, пока не выпадет орел. Или наоборот, это уж как договоритесь на старте и какую сторону монетки назначите выигрышной.
Прогрессия отсчитывается от размера вашего первоначального взноса, т.е. если вы внесли 1 рубль, он и удваивается, затем умножается на 4, 8, 16, 32 и т.д. Если внесли 100 рублей, значит, с каждой решкой выигрыш становится 200, 400, 800, 1600 и более рублей. Играть можно неограниченное количество раз, каждый раз делая новую ставку. Что скажете? Стоит попробовать или очередной лохотрон?
В общем-то, есть, над чем задуматься. А вот прошли бы нашу обучающую программу «Когнитивистика», где за несколько недель можно освоить прогрессивные техники мышления и научиться находить решения для самых нестандартных задач, вы бы сейчас точно знали, что вам делать! Ну, да не будем о грустном, тем более что вы всегда можете наверстать это упущение и записаться на обучение. Давайте лучше поговорим про Санкт-Петербургский парадокс. Именно на нем и основана описанная нами игра.
Что такое Санкт-Петербургский парадокс?
Итак, в чем же заключается Санкт-Петербургский парадокс? В чем его смысл? И что такое Санкт-Петербургский парадокс простыми словами? Парадокс заключается в том, что люди сравнительно легко соглашаются сыграть в игру, если ставка первоначального взноса невелика и возможный выигрыш, соответственно, тоже. И почти всегда отказываются от участия, если ставка высока, а вероятный выигрыш весьма солиден.
А ведь если количество сеансов игры неограниченно, выигрыш практически гарантирован! Во всяком случае, так утверждают исследователи, которые потрудились смоделировать игру и проверить Санкт-Петербургский парадокс эмпирически [Д. Демахин, 2020]. Тем, кто считает представленную проверку чередой случайностей, предлагается скачать файл и подставить любые другие значения ставок и сделать любое другое количество серий игры:
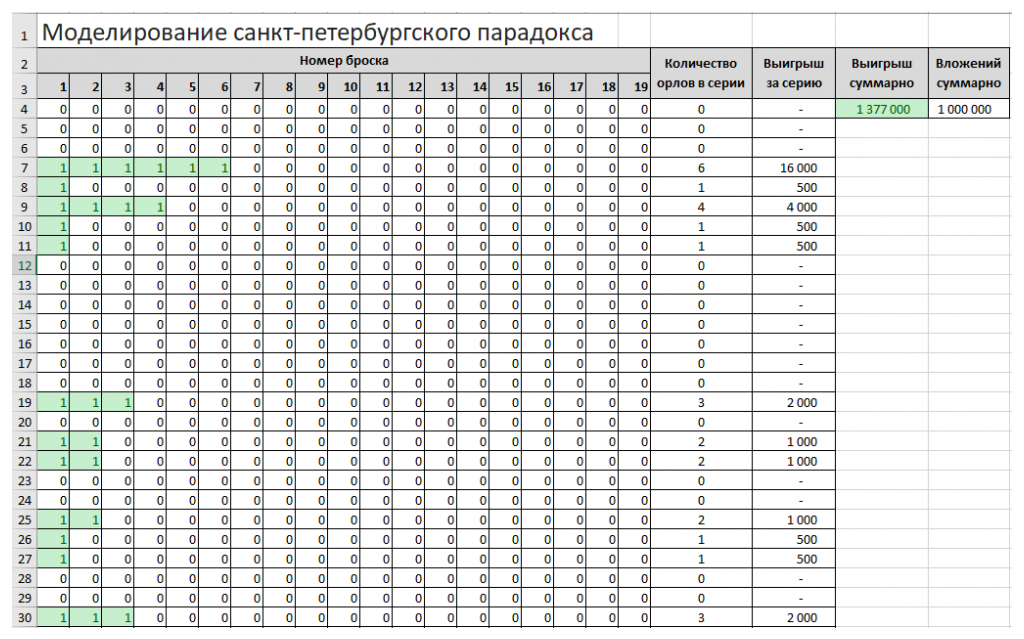
Как заверяет разработчик модели, первое же попадание в длинную последовательность падения монеты «денежной» стороной компенсирует предыдущие неудачные сеансы игры, а суммарный выигрыш больше, чем сумма всех ранее сделанных ставок.
Это эмпирическая модель парадокса. А что же говорит самая точная из всех наук математика? Коль скоро мы взялись объяснять Санкт-Петербургский парадокс простыми словами, не будем отступать от взятых на себя обязательств и попытаемся максимально упростить математические расчеты. Примем вероятность выигрыша за π и рассмотрим его для ставки в 1 рубль. По теории вероятности, шанс падения монетки той или иной стороной составит 50% или 0,5 для каждого броска.
Таким образом, математическое ожидание выигрыша при 1-м броске будет π × 1 руб. или 0,5 × 1 руб. = 0,5 руб. При 2-м броске это ожидание составит (0,5 × 0,5) × 2 руб. = 0,5 руб. Суммарный размер ожидаемого выигрыша – это сумма ожиданий после каждого броска. При неограниченном количестве попыток сумма ожидаемого выигрыша составит 0,5 руб. + 0,5 руб. + 0,5 руб. + ... = ∞ (∞ – это знак бесконечности).
Как видим, при неограниченном количестве сеансов игры выигрыш может быть бесконечно большим. Однако большинство людей не способно заглянуть так далеко и от игры обычно отказывается. В этом и заключается парадокс.
Полные (не упрощенные – гуманитариям не смотреть!) расчеты представлены в статье доктора экономических наук Андрея Кудрявцева «Санкт-Петербургский парадокс и его значение для экономической теории», написанной в 2013 году и приуроченной к 100-летию этого явления [А. Кудрявцев, 2013]. Там же можно найти и ответ на вопрос, почему парадокс называется Санкт-Петербургским.
История Санкт-Петербургского парадокса
Идею Санкт-Петербургского парадокса впервые сформулировал швейцарский математик Николай Бернулли (1687-1759) в письме к своему коллеге из Франции Пьеру Ремону де Монмору (1678-1719). Это случилось в 1713 году, как раз когда готовилось к печати второе издание книги Пьера Ремона де Монмора Essay d'analyse sur les jeux de hazard («Опыт исследования азартных игр») [P. Rémond, 1713]. Правда, в том письме Николай Бернулли предлагал использовать игральные кости, а не монетку, но суть идеи это не меняет.
Ремон опубликовал переписку со своим молодым коллегой в приложении ко второму изданию книги Essay d'analyse sur les jeux de hazard, сделав эту идею достоянием широкой научной общественности. Наибольший интерес идея парадокса вызывала среди математиков, исследовавших теорию вероятности.
Законченный вид формулировки парадокса и получившие признание варианты его решения предложил швейцарский физик и математик Даниил Бернулли (1700-1782), связанный, кстати, родственными связями с Николаем Бернулли. В 1738 году в пятом томе «Комментариев Петербургской Академии наук», где тогда работал Даниил Бернулли, появилась его работа Specimen theoriae novae de mensura sortis («Опыт новой теории измерения жребия»), которая переиздается с незначительными сокращениями по сей день [Д. Бернулли, 1999].
Таким образом, Санкт-Петербургский парадокс Бернулли получил свое название по месту работы автора, чье описание и варианты решений получили наибольшее признание. Произошло это в 1768 году с легкой руки французского физика, математика и философа Жана Лерона Д’Аламбера (1717-1783), назвавшего по-прежнему широко обсуждаемый в научных кругах парадокс Санкт-Петербургским. Название закрепилось и используется до сих пор.
Даже притом, что автор Санкт-Петербургского парадокса Николай Бернулли никогда не работал в «Северной Пальмире», название вполне справедливо, потому что оно отдает дань уважения двум великим ученым, благодаря которым широкая общественность получила в свое распоряжение столь занимательную головоломку.
Основные варианты решения Санкт-Петербургского парадокса
Как мы уже начали обсуждать в нашем историческом экскурсе, Санкт-Петербургский парадокс вызвал большой резонанс в ученой среде, поэтому на протяжении многих лет научных дискуссий было предложено немало вариантов решений парадокса. И мы уже знаем, что наибольшее признание получил вариант, предложенный Даниилом Бернулли.
Он предложил решить этот парадокс в контексте теории ожидаемой полезности. Мы взялись объяснять Санкт-Петербургский парадокс простыми словами, поэтому просто скажем, что, по мнению Даниила Бернулли, стоимость чего-либо (предмета, выигрыша) основана не собственно на абсолютной цене, а на той полезности, что принесет предмет или выигрыш.
На этом основании Даниил Бернулли предложил презумпцию убывающей предельной полезности денег. Простыми словами, некая сумма финансов будет иметь гораздо большую ценность для нищего, нежели точно такое же количество денег для богача. Именно поэтому богач не заинтересуется игрой ввиду хлопотности и не такой уж большой ценности выигрыша, а бедняк побоится рисковать последними деньгами. Полные расчеты представлены в работе «Опыт новой теории измерения жребия» [Д. Бернулли, 1999].
Сам автор Санкт-Петербургского парадокса Николай Бернулли предлагал решать задачу через идею взвешенных вероятностей. Проще говоря, он полагал, что люди склонны рассматривать маловероятные события как невозможные. Поскольку ожидать длинную последовательность падения монеты «денежной» стороной с первого или второго сеанса игры маловероятно, люди не рискуют играть «в долгую». В общем-то, они боятся потерять и не отыграть даже свой первоначальный взнос.
Эта гипотеза изначально показалась научной общественности малоубедительной, и видимо поэтому парадокс не стал «швейцарским» по месту жительства автора Николая Бернулли. Зато идея взвешенных вероятностей заинтересовала исследователей спустя многие десятилетия уже в 20 веке. Правда, эта идея вызвала не столько поддержку, сколько критику.
Санкт-Петербургский парадокс в 20-21 веках: исследования и критика
Интерес к исследованиям Санкт-Петербургского парадокса не уменьшился и в последующие после открытия годы. Математики и экономисты из разных стран по-прежнему исследуют прикладные аспекты Санкт-Петербургского парадокса, в том числе применительно к различным аспектам экономики и психологии.
Так, один из основоположников поведенческой экономики американский психолог израильского происхождения Даниель Канеман пришел к выводу, что большинство людей как раз преувеличивает, а не преуменьшает вероятность наступления маловероятных событий. Это нашло отражение в совокупной (кумулятивной) теории перспектив, которая, по сути, есть обобщение теории ожидаемой полезности и над которой Канеман работал совместно со своим израильским коллегой Амосом Тверски.
Свои выводы они оформили в ряде совместных работ. В частности, в работе Availability: A heuristic for judging frequency and probability («Доступность: эвристика для оценки частоты и вероятности») [A. Tversky, D. Kahneman, 1973]. Далее они развили исследования в работе Judgment under Uncertainty: Heuristics and Biases («Суждение в условиях неопределенности: эвристика и предвзятость») и многих других [A. Tversky, D. Kahneman, 1974].
В наши дни Санкт-Петербургский парадокс вызывает большой интерес применительно к азартным играм. Собственно, мы помним, что изначально автор Санкт-Петербургского парадокса Николай Бернулли предлагал использовать игральные кости, а не монету, так что азарт можно считать одной из базовых эмоций для развития понимания сути парадокса.
Среди исследователей современности, изучающих Санкт-Петербургский парадокс применительно к азартным играм, можно отметить Антонио Каппиелло. Особенно показательна его работа Decision making and Saint Petersburg paradox focusing on heuristic parameters, considering the non-ergodic context and the gambling risks («Принятие решений и Санкт-Петербургский парадокс: акцент на эвристических параметрах, с учетом неэргодического контекста и игровых рисков») [A. Cappiello, 2016].
Если сказать простыми словами, Каппиелло считает, что многие люди принимают решения совершенно нерационально и тот же Санкт-Петербургский парадокс воспринимают не совсем верно. Поэтому в своей статье он предлагает некоторые советы, как избежать ловушки бесконечного математического ожидания и учесть все возможные ограничения в любых азартных играх с бесконечным числом повторений [A. Cappiello, 2016].
В разные годы предпринималось немало попыток проверить Санкт-Петербургский парадокс на практике, моделируя различные игровые ситуации. В самом начале нашей статьи мы рассмотрели одну из таких моделей. Однако еще почти 100 лет назад в 1937 году американский математик Уильям Феллер (1906-1970) разработал математический подход с элементами эксперимента.
Суть эксперимента в том, чтобы сыграть с достаточно большим числом привлеченных участников и после рассчитать математическое ожидание выигрыша в ходе исследования. По предложенной Феллером методике, когда последовательность ожидаемого размера выигрыша расходится, нужно предположение о неограниченном числе игровых сеансов. А когда ограничение на число попыток установлено изначально, математическое ожидание сходится к некоему заметно меньшему показателю, чем при бесконечном количестве попыток. Подробнее о методе можно прочитать во «Введении в теорию вероятностей» [У. Феллер, 1984].
Некоторые исследователи предлагают вовсе отказаться от использования метода математического ожидания и основ теории вероятностей для решения Санкт-Петербургского парадокса. Например, английский экономист Джон Мейнард Кейнс (1883-1946) создал свою теорию вероятности, основанную на постулате, что вероятность является в большей степени логическим, нежели числовым отношением. Таким образом, утверждение, включающее вероятностные отношения, обладает значением истинности, независимым от мнения. Свои взгляды он изложил в работе A Treatise on Probability («Трактат о вероятности») [M. Keynes, 2004].
В частности, он наглядно разбирает ситуацию, что, если гипотеза имеет хотя бы наименьшую конечную вероятность, ее можно превратить в достоверность с помощью достаточного количества наблюдений. Применительно к Санкт-Петербургскому парадоксу Кейнс делает вывод, что, если предложить начальный взнос для участия в вышеописанной игре 25 дукатов (дукат – серебряная либо позолоченная монета весом 3,4-3,5 граммов, имевшая хождение в Европе в 13-19 веках), большинство игроков откажутся, посчитав, что они вряд ли смогут выиграть сумму большую, чем вступительный взнос.
Так или иначе, ученые по сей день возвращаются к теме Санкт-Петербургского парадокса, однако единого и удовлетворяющего всех решения пока нет. По крайней мере, так считает ученый-исследователь из Университета Монпелье во Франции Павел Блаватский, что нашло отражение в его статье Back to the St. Petersburg paradox? («Назад к Санкт-Петербургскому парадоксу?») [П. Блаватский, 2005].
К слову, в 2020 году Павел Блаватский взорвал постсоветское информационное пространство своим исследованием взаимосвязи индекса массы тела чиновников и уровня коррупции в стране. Результаты исследований обошли многие средства массовой информации [Inshe.tv, 2020]. Интересен не только вывод ученого, что чем толще политики, тем стройнее избиратели и тем выше уровень коррупции, но и предположение, что коррупция может быть полезна обществу, т.к. способствует снижению индекса массы тела и улучшению здоровья широких слоев населения.
Это мы чуть-чуть отвлеклись и надеемся, что вы не потеряли мысль. И уже готовы задуматься вместе с нами: а что же такого важного и значимого таит в себе Санкт-Петербургский парадокс, что до сих пор приковывает к себе внимание научной общественности? Ну, кроме того, что он занимателен и интересен сам по себе? Давайте посмотрим!
Значение Санкт-Петербургского парадокса
Первое и главное, это, конечно же, использование подходов к решению Санкт-Петербургского парадокса для просчета шансов выиграть в азартной игре с повторяющимися действиями. Причем в 18 столетии, когда родился этот парадокс, данная тема занимала в большей степени умы математиков, а не самих игроков.
Так, уже упоминавшийся в нашей статье французский физик, философ и математик Жан Лерон Д’Аламбер предложил свою финансовую интерпретацию парадокса, которая получила название «мартингал Д’Аламбера». Суть в том, что, к примеру, при игре в рулетку нужно ставить всегда на один цвет и при каждом проигрыше удваивать ставку. По Д’Аламберу, такой подход, рано или поздно, приведет к выигрышу. В практическом преломлении это, скорее, приведет к тому, что у игрока очень быстро закончатся деньги.
Подробнее с идеями Д’Аламбера можно ознакомиться в его Оeuvres complètes («Полном собрании сочинений»), вышедшем под редакцией Ирен Пассерон, специалиста по истории науки из Франции [J. D'Alembert, 2009]. Выборочно расчеты Д’Аламбера представлены в статье «Санкт-Петербургский парадокс и его значение для экономической теории» [А. Кудрявцев, 2013].
Вот тут мы подошли ко второму и не менее важному аспекту Санкт-Петербургского парадокса. А именно к его значению для развития экономической теории. Отметим, что авторы Санкт-Петербургского парадокса не пытались применить свои расчеты для каких-либо макроэкономических схем, хотя и демонстрировали экономические приложения парадокса. Этот потенциал увидели и оценили ученые-экономисты спустя столетия.
Как вы помните, Даниил Бернулли предложил презумпцию убывающей предельной полезности денег, когда одна и та же сумма более ценна для нищего, но уже не так критична для богача. С развитием экономики, финансовых рынков и банковской системы эти идеи стали основой исследований для ученых-теоретиков, на их основе пытались строить финансовые модели представители страховой и многих других сфер. В качестве примера можно привести статью Дэвида Дюрана Growth stocks and the Petersburg paradox («Акции роста и Петербургский парадокс») [D. Durand, 1957].
Подробнее о направлениях экономической мысли, стимулированных исследованиями Санкт-Петербургского парадокса, можно прочитать в работе австрийского экономиста, основателя австрийской школы в экономике Карла Менгера (1840-1921) Das Unsicherheitsmoment in der Wertlehre («Элемент неопределенности в теории ценностей» [К. Menger, 1934]. К слову, по Менгеру, истинный смысл Санкт-Петербургского парадокса состоит в несоответствии математической модели и наблюдаемого поведения. Более простым языком и короче экономические аспекты Санкт-Петербургского парадокса изложены в статье «Даниил Бернулли – экономист» [П. Ватник, 2008].
А мы подытожим, где же могут быть полезны основы и решения Санкт-Петербургского парадокса:
- Просчет вероятности выигрыша в азартных играх.
- Просчет вероятности наступления страхового случая.
- Моделирование финансовых процессов в банковской сфере.
- Исследования в области поведенческой экономики.
- Прикладные аспекты теории вероятности.
Возможно, вы сможете дополнить и расширить этот список, если пройдете нашу обучающую программу «Когнитивистика», где за несколько недель можно освоить прогрессивные техники мышления и научиться находить решение для самых нестандартных задач.
Желаем удачи!
А еще нам интересно:
