Круги Эйлера представляют собой особую геометрическую схему, необходимую для поиска и более наглядного отображения логических связей между понятиями и явлениями, а также для изображения отношений между определенным множеством и его частью. Благодаря наглядности они значительно упрощают любые рассуждения и помогают быстрее находить ответы на вопросы.
Автором кругов является известный математик Леонард Эйлер, который считал, что они необходимы, чтобы облегчить размышления человека. С момента своего появления метод приобрел широкую популярность и признание.
Позже круги Эйлера использовали в своих работах многие известные ученые, к примеру, чешский математик Бернард Больцано, немецкий математик Эрнест Шредер, английский философ и логик Джон Венн и другие. Сегодня методика служит основной многих упражнений на развитие мышления, в том числе и упражнений из нашей бесплатной онлайн-программы «Нейробика».
Для чего нужны круги Эйлера
Круги Эйлера имеют прикладное значение, ведь с их помощью можно решать множество практических задач на пересечение или объединение множеств в логике, математике, менеджменте, информатике, статистике и т.д. Полезны они и в жизни, т.к., работая с ними, можно получать ответы на многие важные вопросы, находить массу логических взаимосвязей.
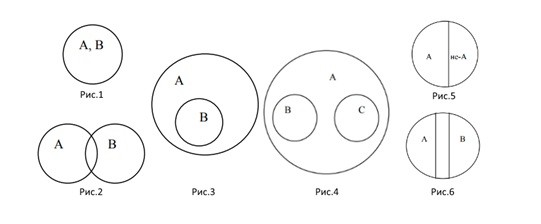
Есть несколько групп кругов Эйлера:
- равнозначные круги (рисунок 1 на схеме);
- пересекающиеся круги (рисунок 2 на схеме);
- подчиненные круги (рисунок 3 на схеме);
- соподчиненные круги (рисунок 4 на схеме);
- противоречащие круги (рисунок 5 на схеме);
- противоположные круги (рисунок 6 на схеме).
Посмотрите схему:
Но в упражнениях на развитие мышления чаще всего встречаются два вида кругов:
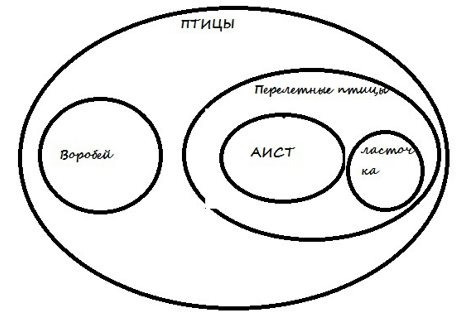
- Круги, описывающие объединения понятий и демонстрирующие вложенность одного в другое. Посмотрите пример:
- Круги, описывающие пересечения разных множеств, имеющих некоторые общие признаки. Посмотрите пример:
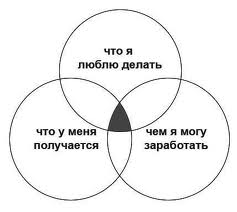
Результат использования кругов Эйлера проследить на этом примере очень просто: обдумывая, какую профессию выбрать, вы можете либо долго рассуждать, пытаясь понять, что больше подойдет, а можете нарисовать аналогичную диаграмму, ответить на вопросы и сделать логический вывод.
Применять метод очень просто. Также его можно назвать универсальным – подходящим для людей всех возрастов: от детей дошкольного возраста (в детских садах детям преподают круги, начиная с 4-5-летнего возраста) до студентов (задачи с кругами есть, к примеру, в тестах ЕГЭ по информатике) и ученых (круги широко применяются в академической среде).
Типичный пример кругов Эйлера
Чтобы вы могли лучше понять, как «работают» круги Эйлера, рекомендуем познакомиться с типичным примером. Обратите внимание на нижеследующий рисунок:
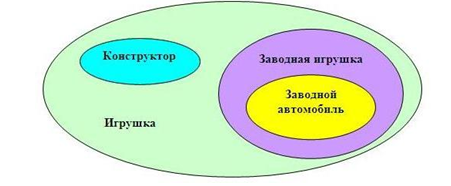
На рисунке зеленым цветов отмечено наибольшее множество, представляющее собой все варианты игрушек. Один из них – это конструкторы (голубой овал). Конструкторы – это отдельное множество само по себе, но в то же время и часть общего множества игрушек.
Заводные игрушки (фиолетовый овал) тоже относятся к множеству игрушек, однако к множеству конструктора они отношения не имеют. Зато заводной автомобиль (желтый овал), пусть и является самостоятельным явлением, но считается одним из подмножеств заводных игрушек.
По подобной схеме строятся и решаются многие задачи (включая и задания на развитие когнитивных способностей), задействующие круги Эйлера. Давайте разберем одну такую задачу (кстати, именно ее в 2011 году внесли на демонстрационный тест ЕГЭ по информатике и ИКТ).
Пример решения задачи с помощью кругов Эйлера
Условия задачи таковы: приведенная таблица показывает, сколько страниц было найдено в Интернете по конкретным запросам:
| Запрос | Найдено страниц (в тысячах) |
| Крейсер/линкор | 7 000 |
| Крейсер | 4 800 |
| Линкор | 4 500 |
Вопрос задачи: сколько страниц (в тысячах) выдаст поисковик по запросу «Крейсер и линкор»? При этом нужно учитывать, что все запросы выполняются примерно в одно и то же время, поэтому набор страниц с искомыми словами со времени выполнения запросов остался неизменным.
Решается задача так: с помощью кругов Эйлера изображаются условия задачи, а цифрами «1», «2» и «3» обозначаются полученные в результате сегменты:
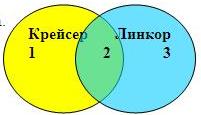
Учитывая условия задачи, составляем уравнения:
- Крейсер/линкор: 1+2+3 = 7 000;
- Крейсер: 1+2 = 4 800;
- Линкор: 2+3 = 4 500.
Чтобы определить количество запросов «Крейсер и линкор» (сегмент обозначен цифрой «2» на рисунке), подставим в уравнение 1 уравнение 2 и получим: 4 800 + 3 = 7 000, а значит, что 3 = 2 200 (т.к. 7 000-4 800 = 2 200).
Далее полученный результат подставляем в уравнение 3 и получаем: 2 + 2 200 = 4 500, а это означает, что 2 = 2 300 (т.к. 4 500-2 200 = 2 300).
Ответ: по запросу «Крейсер и линкор» будет найдено 2 300 страниц.
Этот пример наглядно демонстрирует, что с помощью кругов Эйлера можно достаточно быстро и просто решать сложные задачи.
Резюме
Круги Эйлера – это очень полезная методика решения задач и установления логических связей, а заодно и занимательный и интересный способ провести время и потренировать мозг. Так что, если вам хочется совместить приятное с полезным и поработать головой, предлагаем пройти наш курс «Нейробика», включающий в себя самые разные задания, в том числе и круги Эйлера, эффективность которых научно обоснована и подтверждена многолетней практикой.
